1、Wide&Deep模型
Wide & Deep于2016年google在发表在DLRS 2016上的论文《Wide & Deep Learning for Recommender Systems》提出。Wide&Deep的核心思想是结合线性模型的记忆能力和DNN泛化能力,进而提升模型的整体性能。
1.1 背景
推荐系统的主要挑战之一,是同时解决Memorization和Generalization,理解这两个概念是理解全文思路的关键,下面分别进行解释。
Memorization:面对拥有大规模离散sparse特征的CTR预估问题时,将特征进行非线性转换,然后再使用线性模型是在业界非常普遍的做法,最流行的即「LR+特征叉乘」。Memorization 通过一系列人工的特征叉乘(cross-product)来构造这些非线性特征,捕捉sparse特征之间的高阶相关性,即“记忆” 历史数据中曾共同出现过的特征对。
典型代表是LR模型,使用大量的原始sparse特征和叉乘特征作为输入,很多原始的dense特征通常也会被分桶离散化构造为sparse特征。这种做法的优点是模型可解释高,实现快速高效,特征重要度易于分析,在工业界已被证明是很有效的。Memorization的缺点是:
- 需要更多的人工设计;
- 可能出现过拟合。可以这样理解:如果将所有特征叉乘起来,那么几乎相当于纯粹记住每个训练样本,这个极端情况是最细粒度的叉乘,我们可以通过构造更粗粒度的特征叉乘来增强泛化性;
- 无法捕捉训练数据中未曾出现过的特征对。
Generalization:Generalization 为sparse特征学习低维的dense embeddings 来捕获特征相关性,学习到的embeddings 本身带有一定的语义信息。可以联想到NLP中的词向量,不同词的词向量有相关性,因此文中也称Generalization是基于相关性之间的传递。这类模型的代表是DNN和FM。
- 优点:更少的人工参与,对历史上没有出现的特征组合有更好的泛化性 。
- 缺点:但在推荐系统中,当user-item matrix非常稀疏时,例如有和独特爱好的users以及很小众的items,NN很难为users和items学习到有效的embedding。这种情况下,大部分user-item应该是没有关联的,但dense embedding 的方法还是可以得到对所有 user-item pair 的非零预测,因此导致 over-generalize并推荐不怎么相关的物品。此时Memorization就展示了优势,它可以“记住”这些特殊的特征组合。
Memorization根据历史行为数据,产生的推荐通常和用户已有行为的物品直接相关的物品。而Generalization会学习新的特征组合,提高推荐物品的多样性。 论文作者结合两者的优点,提出了一个新的学习算法——Wide & Deep Learning,其中Wide & Deep分别对应Memorization & Generalization。
1.2 模型结构
Wide & Deep模型结合了LR和DNN,其框架图如下所示。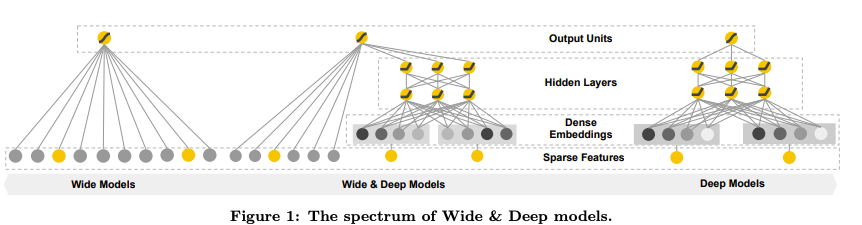
Wide 该部分是广义线性模型,即$y=W^{T}[x,\phi(x)]+b$,其中$x$和$\phi(x)$表示原始特征与叉乘特征。
Deep 该部分是前馈神经网络,网络会对一些sparse特征(如ID类特征)学习一个低维的dense embeddings(维度量级通常在O(10)到O(100)之间),然后和一些原始dense特征一起作为网络的输入。每一层隐层计算:
$a^{l+1}=f(W^{l}a^{l}+b^{l})$,其中$a^{l},b^{l},W^{l}$是第$l$层的激活值、偏置和权重,$f$是激活函数。
损失函数 模型选取logistic loss作为损失函数,此时Wide & Deep最后的预测输出为:
$$p(y=1|x)=\sigma(W^{T}_{wide}[x,\phi(x)]+W^{T}_{deep}a^{l_{f}}+b)$$
其中$\sigma$表示sigmoid函数,$\phi(x)$表示叉乘特征,$a^{l_{f}}$表示NN最后一层激活值。
1.3 联合训练
联合训练(Joint Training)和集成(Ensemble)是不同的,集成是每个模型单独训练,再将模型的结果汇合。相比联合训练,集成的每个独立模型都得学得足够好才有利于随后的汇合,因此每个模型的model size也相对更大。而联合训练的wide部分只需要作一小部分的特征叉乘来弥补deep部分的不足,不需要 一个full-size 的wide 模型。
在论文中,作者通过梯度的反向传播,使用 mini-batch stochastic optimization 训练参数,并对wide部分使用带L1正则的Follow- the-regularized-leader (FTRL) 算法,对deep部分使用 AdaGrad算法。
1.4 总结
- 详细解释了目前常用的 Wide 与 Deep 模型各自的优势:Memorization 与 Generalization。
- 结合 Wide 与 Deep 的优势,提出了联合训练的 Wide & Deep Learning。相比单独的 Wide / Deep模型,实验显示了Wide & Deep的有效性,并成功将之成功应用于Google Play的app推荐业务。
- 目前Wide 结合 Deep的思想已经非常流行,结构虽然简单,从业界的很多反馈来看,合理地结合自身业务借鉴该结构,实际效果确实是efficient。
1.5 参考
2、FM算法
FM算法2010年由Rendle提出的,但是真正在各大厂大规模在CTR预估和推荐领域广泛使用,其实也就是最近几年的事。paper地址。
在计算广告和推荐系统中,CTR预估(click-through rate)是非常重要的一个环节,判断一个物品是否进行推荐需要根据CTR预估的点击率排序决定。业界常用的方法有人工特征工程 + LR(Logistic Regression)、GBDT(Gradient Boosting Decision Tree) + LR、FM(Factorization Machine)和FFM(Field-aware Factorization Machine)模型。
最近几年出现了很多基于FM改进的方法,如deepFM,FNN,PNN,DCN,xDeepFM等。
2.1 FM优缺点
FM(factor Machine,因子分解机)算法是一种基于矩阵分解的机器学习算法,是为了解决大规模稀疏矩阵中特征组合问题。
为什么需要FM呢?
特征组合是许多机器学习建模过程中遇到的问题,如果直接建模,可能忽略特征与特征之间的关联信息,因此,可通通过构建新的交叉特征 这一特征组合方式提高模型效果。其实就是增加特征交叉项。
在一般的线性模型中,是各个特征独立思考的,没有考虑到特征之间的相互关系。但是实际上,大量特征之间是关联。 一般女性用户看化妆品服装之类的广告比较多,而男性更青睐各种球类装备。那很明显,女性这个特征与化妆品类服装类商品有很大的关联性,男性这个特征与球类装备的关联性更为密切。如果我们能将这些有关联的特征找出来,显然是很有意义的。
高维的稀疏矩阵是实际工程中常见的问题,并直接会导致计算量过大,特征权重更新缓慢。而FM的优势,就是在于这两方面问题的处理。首先是特征组合,通过两两特征组合,引入交叉特征,提高模型得分。其次是高维灾难,通过引入隐向量,对特征参数进行估计。
可以在非常稀疏的数据中进行合理的参数估计;FM模型的时间复杂度是线性的;FM是一个通用模型,它可以用于任何特征为实值的情况;同时解决了特征组合问题。
引入FM的目的:旨在解决稀疏数据下的特征组合问题。优势:高度稀疏的数据场景具有线性计算复杂度。
- FM的优点:可以在非常稀疏的数据中,进行合理的参数估计;FM模型的复杂度是线性的,优化效果好,不需要像svm一样依赖于支持向量;FM是一个通用的模型,他咳哟用于任何特征为实值得情况。而其他得因式分解模型只能用于一些输入数据比较固定得情况。
但是FM也有其缺点,就是组合特征的泛化性比较差。
2.2 FM特征组合
多项式模型是包含特征组合的最直观的模型。在多项式模型中,特征$x_{i}$和$x_{j}$的组合采用$x_{i}x_{j}$表示,即$x_{i}$和$x_{j}$都为非零时特征组合$x_{i}x_{j}$才有意义。本文只讨论二阶多项式模型,模型的表达式如下:
$$y(X)=w_{0}+\sum^{n}_{i=1}w_{i}x_{i}+\sum^{n}_{i=1}\sum^{n}_{j=n+1}w_{ij}x_{i}x_{j}$$
从公式中,我们可以看出组合特征得参数一共有1/2n(n-1)个,任意两个参数都是独立的。然而在数据稀疏性普遍存在的实际场景中,二次项参数的训练是很困难的。原因是:每个参数wij的训练都需要大量xi 和xj都非零的样本;由于样本数据本来就比较稀疏,满足xi,xj都非零的样本将会非常的少。训练样本不足,很容易导致参数wij不准确,最终将严重影响模型的性能。
那么,交叉项参数的训练问题可以用矩阵分解来近似解决,有下面的公式:
$$y(X)=w_{0}+\sum^{n}_{i=1}w_{i}x_{i}+\sum^{n}_{i=1}\sum^{n}_{j=n+1}<v_{i},v_{j}>x_{i}x_{j}$$
其中模型需要估计的参数是:
$$
w\in R,w \in R^{n},V \in R^{n \times k}
$$
$<\cdot,\cdot>$是两个$K$维向量的内积:
$$<v_{i},v_{j}>=\sum^{k}_{k=1}v_{i,f}v_{j,f}$$
对任意正定矩阵$W$ ,只要$k$足够大,就存在矩阵$W$ ,使得$W=VV^{T}$ 。然而在数据稀疏的情况下,应该选择较小的$k$,因为没有足够的数据来估计$w_{ij}$ 。限制k的大小提高了模型更好的泛化能力。
为什么说可以提高模型的泛化能力呢?
假设我们要计算用户$A$与电影$ST$的交叉项,很显然,训练数据里没有这种情况,这样会导致$w_{A,ST}=0$ ,但是我们可以近似计算出$<V_{A},V_{ST}>$ 。首先,用户$B$ 和$C$ 有相似的向量$V_{B}$ 和$V_{C}$ ,因为他们对$SW$的预测评分比较相似, 所以$<V_{B},V_{SW}>$和$<V_{C},V_{SW}>$是相似的。用户$A$和$C$有不同的向量,因为对$TI$ 和 $SW$的预测评分完全不同。接下来,$ST$和$SW$的向量可能相似,因为用户$B$对这两部电影的评分也相似。最后可以看出,$<V_{A},V_{ST}>$与$<V_{A},V_{SW}>$ 是相似的。
如果按照上述的方式计算特征交叉时间复杂度是$O(kn^{2})$,因为所有的交叉特征都需要计算。但是通过公式变换,可以减少到线性复杂度,方法如下: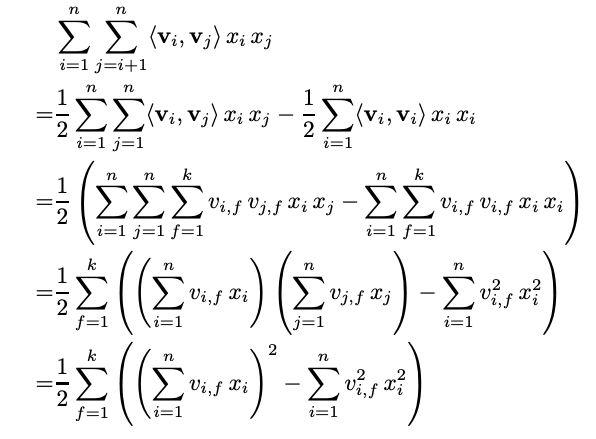
可以看到这时的时间复杂度为$O(kn)$
2.3 FM的预测
FM算法可以应用在多种的预测任务中,包括:
- Regression :$y(X)$可以直接用作预测,并且最小平方误差来优化。
- Binary classification ::$y(X)$作为目标函数并且使用hinge loss或者logit loss来优化。
- Ranking : 向量$X$ 通过$y(X)$的分数排序,并且通过pairwise的分类损失来优化成对的样本$(x^{(a)},x^{(b)})$
对以上的任务中,正则化项参数一般加入目标函数中以防止过拟合。
2.4 FM的参数学习
从上面的描述可以知道FM可以在线性的时间内进行预测。因此模型的参数可以通过梯度下降的方法(例如随机梯度下降)来学习,对于各种的损失函数。FM模型的梯度是:
$$
\frac{\partial }{\partial \theta}\hat{y}(X)=
\begin{cases}
1 & \mbox{if }\theta\mbox{ is }w_{0} \\
x_{i} & \mbox{if }\theta\mbox{ is }w_{i} \\
x_{i}\sum^{n}_{j=1}v_{j,f}x_{i}-v_{i,f}x^{2}_{i} & \mbox{if }\theta\mbox{ is }v_{i,f}
\end{cases}
$$
由于$\sum^{n}_{j=1}v_{j,f}x_{i}$只与$f$有关,与$i$是独立的,可以提前计算出来,并且每次梯度更新可以在常数时间复杂度内完成,因此FM参数训练的复杂度也是$O(kn)$。综上可知,FM可以在线性时间训练和预测,是一种非常高效的模型。
2.5 多阶FM
2阶FM可以很容易泛化到高阶:
$$
y(X)=w_{0}+\sum^{n}_{i=1}w_{i}x_{i}+\sum^{d}_{l=2}\sum^{n}_{i_{1}=1}……\sum^{n}_{i_{l}=i_{l-1}+1}(\prod^{l}_{j=1}x_{ij})(\sum^{k_{l}}_{f=1}\sum^{l}_{j=1}v^{(l)}_{i_{j},f})
$$
其中对第$l$个交互参数是由PARAFAC模型的参数因子分解得到:
$$
V^{(l)}\in R^{n \times k_{l}},k_{l} \in N^{+}_{0}
$$
直接计算公式的时间复杂度是$O(k_{d}n^{d})$ 。通过调整也可以在线性时间内运行。
2.6 总结
FM模型有两个优势:
- 在高度稀疏的情况下特征之间的交叉仍然能够估计,而且可以泛化到未被观察的交叉
- 参数的学习和模型的预测的时间复杂度是线性的
FM模型的优化点:
- 特征为全交叉,耗费资源,通常user与user,item与item内部的交叉的作用要小于user与item的交叉
- 使用矩阵计算,而不是for循环计算
- 高阶交叉特征的构造
2.7 参考
3、DeepFM算法
待更新…
4、xDeepFM算法
待更新…
5、AutoInt算法
待更新…
6、DIN网络
待更新…
7、MLR算法
待更新…
8、NCF算法
待更新…
9、YoutubeNet
待更新…