1、ROC和AUC

如果要理解AUC和ROC曲线，首先要理解混淆矩阵的定义。混淆矩阵中有着Positive、Negative、True、False的概念，其意义如下：

混淆矩阵

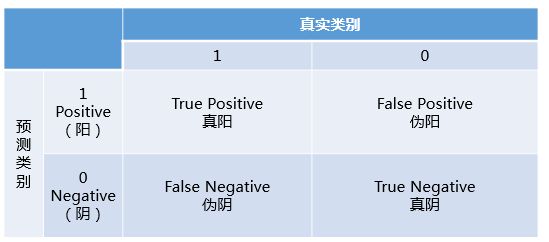
称预测类别为1的为Positive（阳性），预测类别为0的为Negative（阴性）。
预测正确的为True（真），预测错误的为False（伪）。

然后，由此引出True Positive Rate（真阳率）、False Positive（伪阳率）两个概念：

$$TPRate=\frac{ TP }{ TP+FN } $$

$$FPRate= \frac{ FP }{ FP+TN } $$

仔细看这两个公式，发现其实TPRate就是TP除以TP所在的列，FPRate就是FP除以FP所在的列，二者意义如下：

TPRate的意义是所有真实类别为1的样本中，预测类别为1的比例
FPRate的意义是所有真是类别为0的样本中，预测类别为1的比例

按照定义，AUC即ROC曲线下的面积，而ROC曲线的横轴是FPRate，纵轴是TPRate，当二者相等时，即y=x，如下图，表示的意义是：对于不论真实类别是1还是0的样本，分类器预测为1的概率是相等的.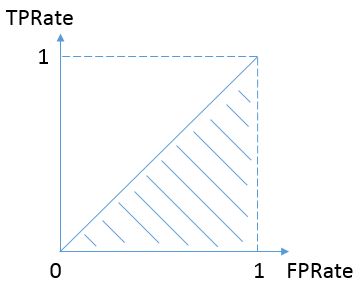

换句话说，和抛硬币并没有什么区别，一个抛硬币的分类器是我们能想象的最差的情况，因此一般来说我们认为AUC的最小值为0.5（当然也存在预测相反这种极端的情况，AUC小于0.5）。
而我们希望分类器达到的效果是：对于真实类别为1的样本，分类器预测为1的概率（即TPRate），要大于真实类别为0而预测类别为1的概率（即FPRate），这样的ROC曲线是在y=x之上的，因此大部分的ROC曲线长成下面这个样子：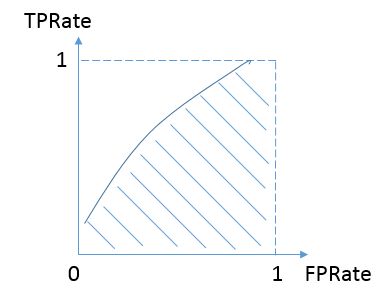

AUC的计算方法同时考虑了分类器对于正例和负例的分类能力，在样本不平衡的情况下，依然能够对分类器作出合理的评价。例如在反欺诈场景，设非欺诈类样本为正例，负例占比很少（假设0.1%），如果使用准确率评估，把所有的样本预测为正例便可以获得99.9%的准确率。但是如果使用AUC，把所有样本预测为正例，TPRate和FPRate同时为1，AUC仅为0.5，成功规避了样本不均匀带来的问题。

auc的真实(物理)含义 :
AUC是指随机给定一个正样本和一个负样本，分类器输出该正样本为正的那个概率值比分类器输出该负样本为正的那个概率值要大的可能性。

2、精确率Precision、召回率Recall和F1值

还是一句上图的混淆矩阵
精确率(precision)定义为:
$$
P=\frac{TP}{TP+FP}
$$

准确率(accuracy)定义为:
$$
P=\frac{TP+TN}{TP+FP+TN+FN}
$$

在正负样本不平衡的情况下，准确率这个评价指标有很大的缺陷。比如在互联网广告里面，点击的数量是很少的，一般只有千分之几，如果用acc，即使全部预测成负类（不点击）acc 也有 99% 以上，没有意义。

召回率(recall,sensitivity,true positive rate)定义为：
$$
R=\frac{TP}{TP+FN}
$$

此外，还有$F_{1}$值，是精确率和召回率的调和均值，
$$
\frac{2}{F_{1}}= \frac{ 1 }{ P } + \frac{ 1 }{ R } \\
F_{1} = \frac{2TP}{2TP+FP+FN}= \frac{2 \ast P \ast R}{P+R}
$$

精确率和准确率都高的情况下，F1 值也会高

精确率（正确率）和召回率是广泛用于信息检索和统计学分类领域的两个度量值，用来评价结果的质量。其中精度是检索出相关文档数与检索出的文档总数的比率，衡量的是检索系统的查准率；召回率是指检索出的相关文档数和文档库中所有的相关文档数的比率，衡量的是检索系统的查全率。

一般来说，Precision就是检索出来的条目（比如：文档、网页等）有多少是准确的，Recall就是所有准确的条目有多少被检索出来了，两者的定义分别如下：

查准率＝检索出的相关信息量 / 检索出的信息总量
查全率＝检索出的相关信息量 / 系统中的相关信息总量

举个例子：

假设我们手上有60个正样本，40个负样本，我们要找出所有的正样本，系统查找出50个，其中只有40个是真正的正样本，计算上述各指标。
TP: 将正类预测为正类数 40
FN: 将正类预测为负类数 20
FP: 将负类预测为正类数 10
TN: 将负类预测为负类数 30

准确率(accuracy) = 预测对的/所有 = (TP+TN)/(TP+FN+FP+TN) = 70%
精确率(precision) = TP/(TP+FP) = 80%
召回率(recall) = TP/(TP+FN) = 2/3

注:精确率(precision)和准确率(accuracy)是不一样的.

3、平均绝对误差和平均平方误差

平均绝对误差
平均绝对误差MAE（Mean Absolute Error）又被称为 l1 范数损失（l1-norm loss）：
$$
MAE(y_{i},\hat{y}_{i})=\frac{1}{n_{samples}}\sum_{i=1}^{n_{samples}}|y_{i}-\hat{y}_{i}|
$$
平均平方误差
平均平方误差 MSE（Mean Squared Error）又被称为 l2 范数损失（l2-norm loss）：
$$
MSE(y_{i},\hat{y}_{i})=\frac{1}{n_{samples}}\sum_{i=1}^{n_{samples}}(y_{i}-\hat{y}_{i})^2
$$

4、ks值

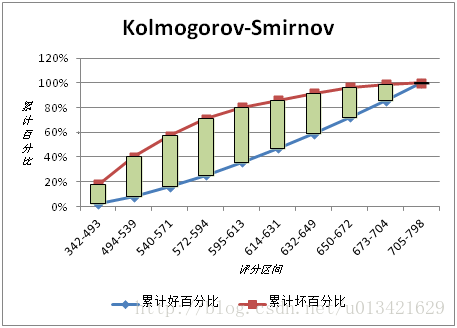
KS(Kolmogorov-Smirnov)：
KS用于模型风险区分能力进行评估,指标衡量的是好坏样本累计分部之间的差值。
好坏样本累计差异越大，KS指标越大，那么模型的风险区分能力越强。
通常来讲，KS>0.2即表示模型有较好的预测准确性。

KS的计算步骤如下：

计算每个评分区间的好坏账户数。
计算每个评分区间的累计好账户数占总好账户数比率(good%)和累计坏账户数占总坏账户数比率(bad%)。
计算每个评分区间累计坏账户占比与累计好账户占比差的绝对值（累计good%-累计bad%），然后对这些绝对值取最大值即得此评分卡的K-S值。

ks的通俗步骤:

按照分类模型返回的概率降序排列
把0-1之间等分N份，等分点为阈值，计算TPR、FPR
对TPR、FPR描点画图即可

5、基尼系数

GINI系数:也是用于模型风险区分能力进行评估。
GINI统计值衡量坏账户数在好账户数上的的累积分布与随机分布曲线之间的面积，好账户与坏账户分布之间的差异越大，GINI指标越高，表明模型的风险区分能力越强。

GINI系数的计算步骤如下：

计算每个评分区间的好坏账户数。
计算每个评分区间的累计好账户数占总好账户数比率（累计good%）和累计坏账户数占总坏账户数比率(累计bad%)。
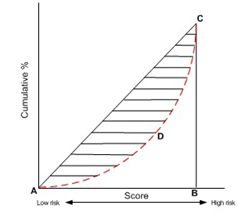
按照累计好账户占比和累计坏账户占比得出下图所示曲线ADC。
计算出图中阴影部分面积，阴影面积占直角三角形ABC面积的百分比，即为GINI系数。

6、困惑度(perplexity)

在信息论中，perplexity(困惑度)用来度量一个概率分布或概率模型预测样本的好坏程度。它也可以用来比较两个概率分布或概率模型。低困惑度的概率分布模型或概率模型能更好地预测样本。
困惑度分为三种：

概率分布的困惑度(Perplexity of a probability distribution)
概率模型的困惑度(Perplexity of a probability model)
每个分词的困惑度(Perplexity per word)

6.1、概率分布的困惑度

定义离散概率分布的困惑度如下：
$$
2^{H(p)}=2^{-\sum_{x}p(x)log_{2}p(x)}
$$
其中H(p)是概率分布p的熵，x是样本点。因此一个随机变量X的困惑度是定义在X的概率分布上的（X所有”可能”取值为x的部分）

一个特殊的例子是k面均匀骰子的概率分布，它的困惑度恰好是k。一个拥有k困惑度的随机变量有着和k面均匀骰子一样多的不确定性，并且可以说该随机变量有着k个困惑度的取值（k-ways perplexed）。

困惑度有时也被用来衡量一个预测问题的难易程度。但这个方法不总是精确的。例如：在概率分布B(1,P=0.9)中，即取得1的概率是0.9，取得0的概率是0.1。可以计算困惑度是：
$$
2^{-0.9log_{2}0.9-0.1log_{2}0.1}=1.38
$$
同时自然地，我们预测下一样本点的策略将是：预测其取值为1，那么我们预测正确的概率是0.9。而困惑度的倒数是1/1.38=0.72而不是0.9。（但当我们考虑k面骰子上的均匀分布时，困惑度是k，困惑度的倒数是1/k，正好是预测正确的概率）

困惑度是信息熵的指数

6.2、概率模型的困惑度

用一个概率模型q去估计真实概率分布p，那么可以通过测试集中的样本来定义这个概率模型的困惑度。
$$
b^{-\frac{1}{N}\sum_{i=1}^{N}log_{b}q(x_{i})}
$$
其中测试样本$x_1, x_2, …, x_N$是来自于真实概率分布p的观测值，b通常取2。因此，低的困惑度表示q对p拟合的越好，当模型q看到测试样本时，它会不会“感到”那么“困惑”。
我们指出，指数部分是交叉熵。
$$
H(\hat{p},q)=-\sum_{x}\hat{p}(x)log_{2}q(x)
$$
其中$\hat{p}$表示我们对真实分布下样本点x出现概率的估计。比如用$p(x)=n/N$

6.3、每个分词的困惑度

在自然语言处理中，困惑度是用来衡量语言概率模型优劣的一个方法。一个语言概率模型可以看成是在整过句子或者文段上的概率分布。
例如每个分词位置上有一个概率分布，这个概率分布表示了每个词在这个位置上出现的概率；或者每个句子位置上有一个概率分布，这个概率分布表示了所有可能句子在这个位置上出现的概率。

比如，i这个句子位置上的概率分布的信息熵可能是190，或者说，i这个句子位置上出现的句子平均要用190 bits去编码，那么这个位置上的概率分布的困惑度就是$2^{190}$。（译者：相当于投掷一个$2^{190}$面筛子的不确定性）通常，我们会考虑句子有不同的长度，所以我们会计算每个分词上的困惑度。比如，一个测试集上共有1000个单词，并且可以用7.95个bits给每个单词编码，那么我们可以说这个模型上每个词有$2^{7.95}=247$困惑度。相当于在每个词语位置上都有投掷一个247面骰子的不确定性。

在Brown corpus (1 million words of American English of varying topics and genres) 上报告的最低的困惑度就是247per word，使用的是一个trigram model（三元语法模型）。在一个特定领域的语料中，常常可以得到更低的困惑度。

要注意的是，这个模型用的是三元语法。直接预测下一个单词是”the”的正确率是7%。但如果直接应用上面的结果，算出来这个预测是正确的概率是1/247=0.4%，这就错了。（译者：不是说算出来就一定是0.4%，而是说这样算本身是错的）因为直接预测下一个词是”the“的话，我们是在使用一元语法，而247是来源于三元语法的。当我们在使用三元语法的时候，会考虑三元语法的统计数据，这样做出来的预测会不一样并且通常有更好的正确率。

机器学习评价指标