回归---线性回归

一、回归

回归是监督学习的一个重要问题，回归用于预测输入变量和输出变量之间的关系。回归模型是表示输入变量到输出变量之间映射的函数。回归问题的学习等价于函数拟合：使用一条函数曲线使其很好的拟合已知函数且很好的预测未知数据,分为模型的学习和预测两个过程,模型学习是基于给定的训练数据集构建一个模型，预测是根据新的输入数据预测相应的输出。
回归的分类：

• 按照输入变量的个数可以分为一元回归和多元回归；
• 按照输入变量和输出变量之间关系的类型，可以分为线性回归和非线性回归

二、线性回归

2.1、介绍

1、单变量线性回归（一元回归）：
形如$h(x)=\theta_0+\theta_1*x_1$,如下图所示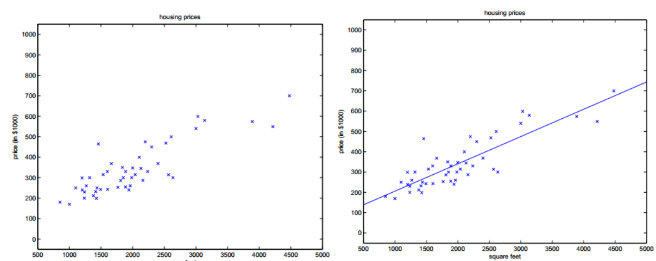

2、多变量线性回归(多元回归)：
形如：$h(x)=\theta_0+\theta_1x_1+\theta_2x_2=\theta^TX$，如下图所示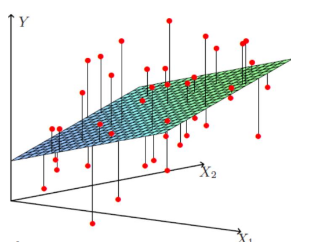

3、多项式回归（Polynomial Regression）：
形如$h(x)=\theta_0+\theta_1x_1+\theta_2x_2^2+\theta_3x_3^3$或者$h(x)=\theta_0+\theta_1x_1+\theta_2\sqrt{x_2}$,但是我们可以令$x_2=x_2^2$，$x_3=x_3^3$，于是又将其转化为了线性回归模型。虽然不能说多项式回归问题属于线性回归问题，但是一般我们就是这么做的。
所以最终通用表达式就是：
$$h_\theta(x)=\theta^TX=\theta_0x_0+\theta_1x_1+\theta_2x_2+\theta_3x_3+….+\theta_nx_n$$

2.2、目标函数

1、依据最小二乘法获取目标函数
我们需要训练一条直线尽量去拟合数据集中的每个点，但是一条直线去拟合所有的点都在这条直线上肯定不现实，所以我们希望这些点尽量离这条直线近一点即去找每个点和直线的距离最小的那条直线。对于每个点直线预测出来的值和实际值都会有一个偏差($y_i-(\theta_0+\theta_1*x_1)$),在训练的过程中目标就是是的loss最小，那么如何最小化误差，使用最小二乘法可以解决该问题:

$$loss=\dfrac{1}{N}\sum_i^N(y_i-(\theta_1x_1+\theta_0))^2=\dfrac{1}{N}\sum_i^m(y^{(i)}-\theta^Tx^{(i)})^2$$

注：最小二乘法又称最小平方法，它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。

2、依据最大似然估计获取目标函数
现在假设我们有m个样本，我们假设有：$y^{(i)}=\theta_Tx^{(i)}+\varepsilon^{(i)}$
误差$\varepsilon^{(i)}$（$ 1\leq i \leq m$）是独立同分布的，服从均值为0，方差为某定制$\sigma^2$的高斯分布，原因：中心极限定理

中心极限定理 的意义：实际问题中，很多随机现象可以看做众多因素的独立影响的综合反应，往往近似服从正态分布，比如：城市耗电量（大量用户的耗电量总和）、测量误差（许多观察不到的微小误差总和）
注：应用前提是多个随机变量的和，有些问题是乘性误差，需要鉴别或者取对数后使用

依据上面的结论，则有:
$$p(\varepsilon^{(i)})=\frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{(\varepsilon^{(i)})^2}{2\sigma^2})$$
带入$\varepsilon^{(i)}$后有：
$$p(y^{(i)}|x^{(i)};\theta)=\frac{1}{\sqrt{2\pi}\sigma}exp(-\dfrac{(y^{(i)}-(\theta^Tx^{(i)}))^2}{2\sigma^2})$$
表示在$\theta$给定的时候，给出一个对应的$x^{(i)}$的时候会算出对应的$y^{(i)}$的概率密度，因为样本是独立同分布，则$p(y_1y_2y_3….y_m)$的联合概率为各自的边缘概率的乘积，则有：
$$L(\theta)=\prod_i^mp(y^{(i)}|x^{(i)};\theta)=\prod_i^m\frac{1}{\sqrt{2\pi}\sigma}exp(-\dfrac{(y^{(i)}-(\theta^Tx^{(i)}))^2}{2\sigma^2})$$
$L(\theta)$即为似然函数。

根据极大似然估计的定义,我们需要$L(\theta)$最大，那么我们怎么才能是的这个值最大呢？两边取对数对这个表达式进行化简如下：

注:在此我们取了一个对数似然，有两点优势，一个就是可以将乘法转换为加法，第二个取对数是单调上升函数，取最大似然和取对数最大似然目标是一致的

需要$L(\theta)$最大，也就是只要满足上述公式中最后一项的后半部分最小。

注：因为对于$L(\theta)$而言变量为$\theta$，所以$mlog\frac{1}{\sqrt{2\pi}\sigma}$是一个常数

则令：

$$J(\theta)=\frac{1}{2}\sum_i^m(y^{(i)}-\theta^Tx^{(i)})^2$$

则若需要$L(\theta)$最大，则只需$J(\theta)$最小即可，则目标函数转换为$J(\theta)$，也即损失函数。

所以，我们最后由极大似然估计推导得出，我们希望 $J(\theta)$最小，而这刚好就是最小二乘法做的工作。而回过头来我们发现，之所以最小二乘法有道理，是因为我们之前假设误差项服从高斯分布，假如我们假设它服从别的分布，那么最后的目标函数的形式也会相应变化。
好了，上边我们得到了有极大似然估计或者最小二乘法，我们的模型求解需要最小化目标函数$J(\theta)$，那么我们的$\theta$到底怎么求解呢？有没有一个解析式可以表示$\theta$?

2.3、目标函数求解

依据上面的推倒，我们已经建立了目标函数，最终我们需要依据目标函数 $J(\theta)$来求解$\theta$即模型的参数。求解方式有两种，一种是解析解，另外一种方式是使用梯度下降的方式求解。

2.3.1、解析解

目标函数为：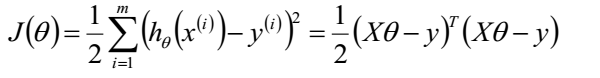

我们需要最小化目标函数，关心$\theta$取什么值的时候使得目标函数取得最小值。而目标函数连续，那么$\theta$一定为目标函数的驻点，所以我们求导寻找驻点。
求导可得：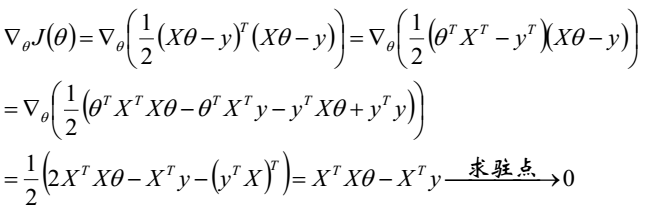

最终我们得到参数 $\theta$的解析式：

$X^TX$ 是一个半正定矩阵，所以若$X^TX$ 不可逆或为了防止过拟合，我们增加$\lambda$扰动，得到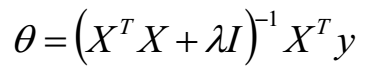

从另一个角度来看，这相当与给我们的线性回归参数增加一个惩罚因子，这是必要的，我们数据是有干扰的，不正则的话有可能数据对于训练集拟合的特别好，但是对于新数据的预测误差很大。

2.3.2、梯度下降求解

上述给出了解析解的求法，如果特征规模很大，超过了1000维，那么矩阵的逆是不方便求的，因此我们可以使用梯度下降算法来做。
求解过程如下：
(1) 初始化θ(随机初始化)
(2) 沿着负梯度方向迭代，更新后的θ使得J(θ)更小：

$$\theta_j=\theta_j-\alpha\frac{\partial J(\theta)}{\partial \theta}$$
其中$\alpha$是步长、学习率，超参数，可以指定一个较小的步长，也可以使用折半查找、回溯、拟牛顿来求一个动态的$\alpha$。然后求解$\frac{\partial J(\theta)}{\partial \theta}$如下：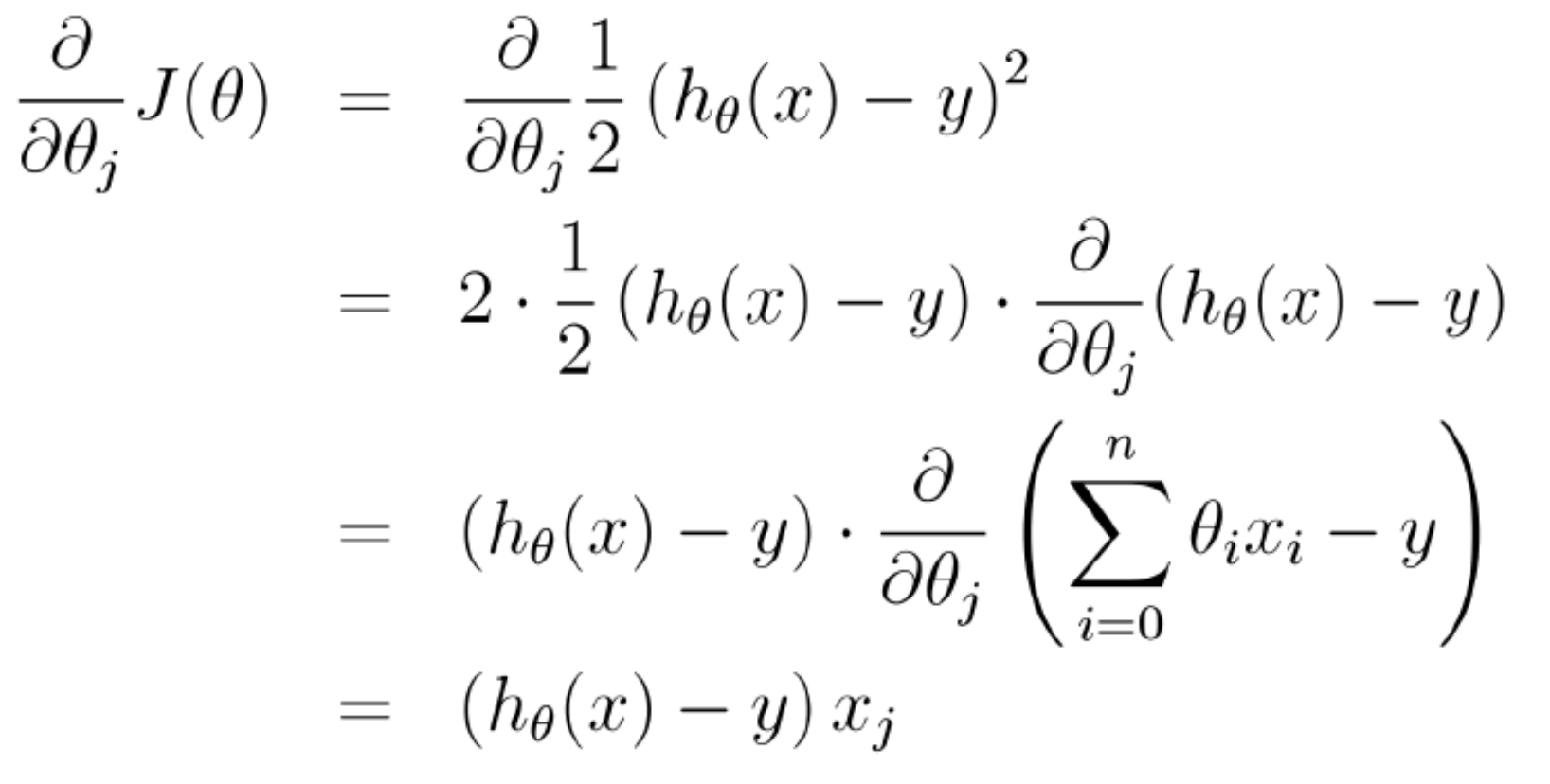

梯度下降是迭代法的一种,可以用于求解最小二乘问题(线性和非线性都可以)。在求解机器学习算法的模型参数，即无约束优化问题时，梯度下降（Gradient Descent）是最常采用的方法之一，另一种常用的方法是最小二乘法。在求解损失函数的最小值时，可以通过梯度下降法来一步步的迭代求解，得到最小化的损失函数和模型参数值。

梯度下降算法分为 批量梯度下降 、随机梯度下降 和 mini-bach梯度下降 方式。

• 批量梯度下降 方式如下：
  
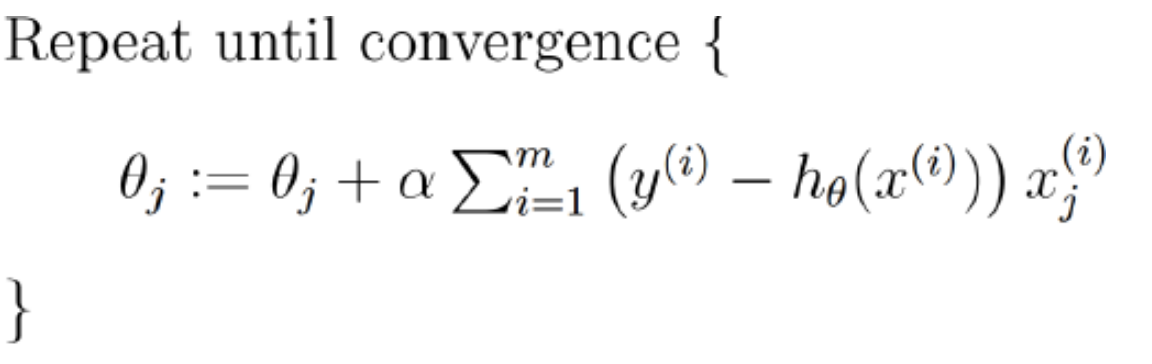
  其中有个∑从i到m加和，也就是说每更新一次都需要那全部的样本做一次梯度下降，这样的话其实效率比较低。

• 随机梯度下降 方式如下：
  
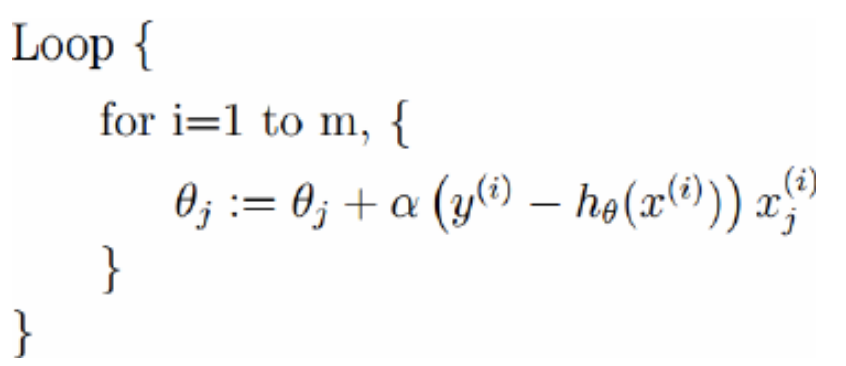
  这种方法每次是拿一个样本来迭代一次梯度，效率会比较高

• mini-bach梯度下降
  每次拿到若干个样本的平均梯度作为更新方向，属于 批量梯度下降 和 随机梯度下降 的折中方式，在CNN中就是使用的该方式。

2.4、解析求解和梯度下降求解对比

梯度下降Gradient Descent	正规方程 Normal Equation
缺点： 1、需要选择学习率$\alpha$ 2、需要多次迭代 3、特征值范围相差太大时，需要特征缩放	优点： 1、不需要选择学习率$\alpha$ 2、不需要多次迭代 3、不需要特征缩放(feature scaling)
优点： 当特征维度n很大时，能够很好工作	缺点： 当特征维度n很大时，运行很慢

三、参考

《统计机器学习方法》–李航
《机器学习课件》–邹博
《Machine Learning》 –Andrew NG