一、前言
岭回归与Lasso回归的出现是为了解决线性回归出现的过拟合以及在通过正规方程方法求解θ的过程中出现的$(X^TX)$不可逆这两类问题的,这两种回归均通过在损失函数中引入正则化项来达到目的。
注:在日常机器学习任务中,如果数据集的特征比样本点还多, $(X^TX)^{-1}$ 的时候会出错。岭回归最先用来处理特征数多于样本数的情况,现在也用于在估计中加入偏差,从而得到更好的估计。这里通过引入$\lambda$限制了所有$\theta^2$之和,通过引入该惩罚项,能够减少不重要的参数,这个技术在统计学上也叫作缩减(shrinkage)。
和岭回归类似,另一个缩减(Shrinkage)LASSO 也加入了正则项对回归系数做了限定。
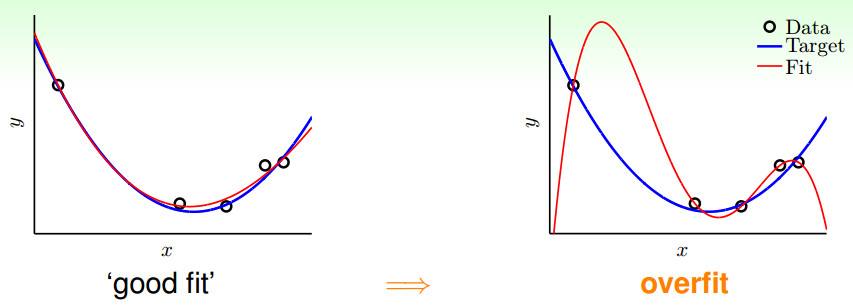
在线性回归中如果参数$\theta$过大、特征过多就会很容易造成过拟合,如下如所示:
二、加入正则
为了防止过拟合(θ过大),在目标函数J(θ)后添加复杂度惩罚因子,即正则项来防止过拟合。正则项可以使用l1-norm(lasso)、l2-norm(Ridge),或结合l1-norm、l2-norm(Elastic Net)。
lasso:使用l1-norm正则
$$J(\theta)=\frac{1}{2}\sum_{i}^{m}(y^{(i)}-\theta^Tx^{(i)})^2+\lambda\sum_{j}^{n}|\theta_j|$$
LASSO有特征选择、降维的作用Ridge:使用l2-norm正则
$$J(\theta)=\frac{1}{2}\sum_{i}^{m}(y^{(i)}-\theta^Tx^{(i)})^2+\lambda\sum_{j}^{n}\theta_j^2$$
- 结合l1-norm、l2-norm进行正则
$$J(\theta)=\frac{1}{2}\sum_{i}^{m}(y^{(i)}-\theta^Tx^{(i)})^2+\lambda(\rho\sum_{j}^{n}|\theta_j|+(1-\rho)\sum_{j}^{n}\theta_j^2)$$
结合了LASSO的特征选择作用,和Ridge较好的效果
三、解释lasso特征选择
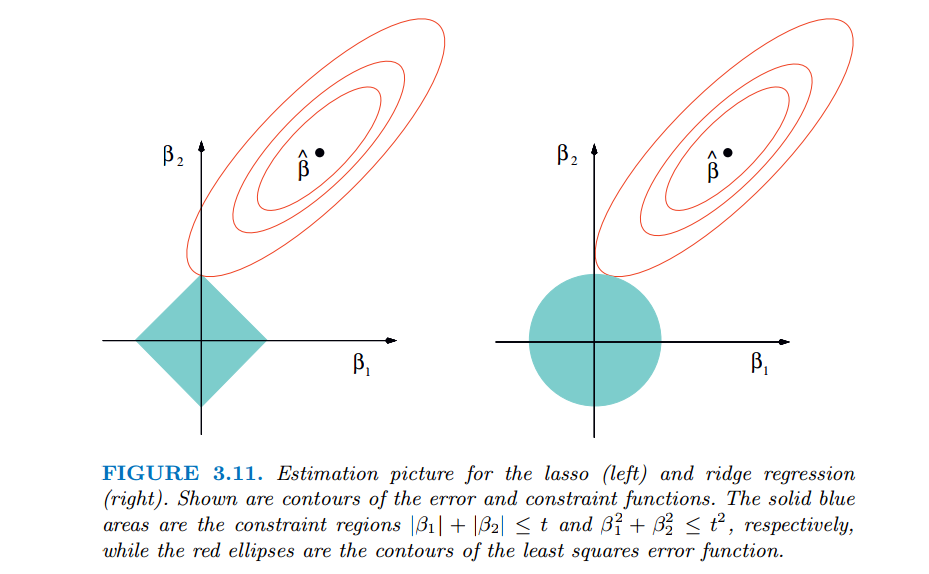
上图中左边为lasso回归,右边为岭回归。红色的椭圆和蓝色的区域的切点就是目标函数的最优解,我们可以看到,如果是圆,则很容易切到圆周的任意一点,但是很难切到坐标轴上,因此没有稀疏;但是如果是菱形或者多边形,则很容易切到坐标轴上,因此很容易产生稀疏的结果。这也说明了为什么L1范式会是稀疏的。这样就解释了为什么lasso可以进行特征选择。
岭回归虽然不能进行特征筛选,但是对$\theta$的模做约束,使得它的数值会比较小,很大程度上减轻了overfitting的问题。
注:岭回归:消除共线性;模的平方处理;Lasso回归:压缩变量,起降维作用;模处理
四、逻辑回归
4.1 模型介绍
在前面我们已经介绍了线性回归,其表达式如下:
$$
z=\theta_0 + \theta_1 x_1 + \theta_2 x_2+….+\theta_n x_n=\theta^T x
$$
而对于Logistic Regression来说,其思想也是基于线性回归(Logistic Regression属于广义线性回归模型)。其公式如下:
$$
h_{\theta}(x)=\frac{1}{1+e^{-z}}=\frac{1}{1+e^{-\theta^{T}x}}
$$
其中$y=\frac{1}{1+e^{-x}}$被称作sigmoid函数,我们可以看到,Logistic Regression算法是将线性函数的结果映射到了sigmoid函数中。sigmoid的函数图形如下: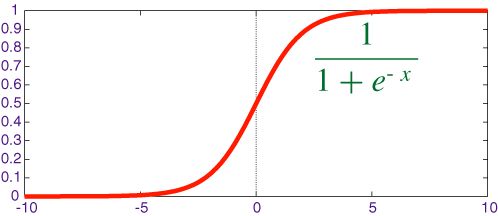
我们可以看到,sigmoid的函数输出是介于(0,1)之间的,中间值是0.5,于是之前的公式$h_{\theta}(x)$的含义就很好理解了,因为$h_{\theta}(x)$输出是介于(0,1)之间,也就表明了数据属于某一类别的概率,例如 :
$h_{\theta}(x)<0.5$ 则说明当前数据属于A类;
$h_{\theta}(x)>0.5$则说明当前数据属于B类。
所以我们可以将sigmoid函数看成样本数据的概率密度函数。
4.2 原理推导
有了上面的公式,我们接下来需要做的就是怎样去估计参数$\theta$了。
$\theta$函数的值有特殊的含义,它表示$h_{\theta}(x)$结果取1的概率,因此对于输入x分类结果为类别1和类别0的概率分别为:
$$
\begin{split}
{} & P(y=1|x;\theta)=h_{\theta}(x) \\
{} & P(y=0|x;\theta)=1-h_{\theta}(x)
\end{split}
$$
接下来可以使用概率论中极大似然估计的方法去求解损失函数,首先得到概率函数为:
$$
P(y|x;\theta)=(h_\theta(x))^y * (1-h_\theta(x))^{1-y}
$$
因为样本数据(m个)独立,所以它们的联合分布可以表示为各边际分布的乘积,取似然函数为:
$$
L(\theta)=\prod_{i=1}^{m}P(y^{(i)}|x^{(i)};\theta)
=\prod_{i=1}^{m}(h_\theta(x^{(i)}))^{y^{(i)}} * (1-h_\theta(x^{(i)}))^{1-y^{(i)}}
$$
取对数似然函数:
$$
\begin{split}
l(\theta)=log(L(\theta)) {} & =\sum_{i=1}^{m}log((h_\theta(x^{(i)}))^{y^{(i)}})+log((1-h_\theta(x^{(i)}))^{1-y^{(i)}}) \\
{} & =\sum_{i=1}^{m}y^{(i)}log(h_\theta(x^{(i)})+(1-y^{(i)})log(1-h_\theta(x^{(i)}))
\end{split}
$$
最大似然估计就是要求得使$l(\theta)$取最大值时的$\theta$,这里可以使用梯度上升法求解。我们稍微变换一下:
$$
J(\theta)=-\frac{1}{m}l(\theta)
$$
因为乘了一个负的系数$-\frac{1}{m}$,然后就可以使用梯度下降算法进行参数求解了。
以上的$l(\theta)便是逻辑回归的损失函数了$
4.3、逻辑回归与交叉熵
线性回归我们采用均方误差(MSE)作为损失函数,而逻辑回归(分类算法)采用交叉熵(Cross Entropy)。逻辑回归得到的$h_{\theta}(x)$可以看作是分类结果的概率。可以这么想,每个样本中的分类结果,在样本空间形成一个结果的分布。当有一个新的样本加入进来,把它对应到样本空间后,可以在已有的分布下对应到它的分类结果。
假设样本的真实分布为sin(x),而我们最开始的假设分布为cos(x),我们的目标是使假设分布无限接近真实分布甚至与真实分布重合。要描述两种分布之间的差异程度,我们引入交叉熵:
概率分布一:p(x) ;概率分布二:q(x)
$$
Hp(q)=\sum p(x)log_{2}^{\frac{1}{q(x)}}=-\sum p(x)log_{2}^{q(x)}
$$
交叉熵描述了两个不同的概率分布p和q的差异程度,两个分布差异越大,则交叉熵的差异越大。详情
交叉熵和熵的关系,它们差异越大,两个分布差异越大,则这两个关系的差异就越大。如果两个分布是一样的,则交叉熵和熵的差异是 0。我们把这个差异叫做相对熵 (Kullback–Leibler divergence), 也叫 KL 距离,KL 散度。Dq(p)=Hq(p)−H(p)。 它就像一个距离度量一样,描述两个概率分布的“距离”
逻辑回归的loss为:$J(\theta)=-[yln(h_{\theta}(x))+(1-y)ln(1-h_{\theta}(x))]$
$h_{\theta}(x)$表示分类结果为1的概率,$1-h_{\theta}(x)$表示分类结果为0的概率。当分类结果为1时,y=1,即真实分布中结果为1的概率是1,结果为0的概率为0。
逻辑回归采用交叉熵作为代价函数,原理就是,模型的分布尽可能的接近样本的概率分布,用这样的模型进行预测才是最优化和最准确的。
交叉熵:
softmax回归的交叉熵损失函数:
$$
CrossEntropy=-\sum_{i=1}^{m}y_ilog(p_i)
$$
其中$p_i$是softmax回归求得的结果,$y_i$是实际的类别