Attention机制和Transformer框架详解

发表于 | 分类于 | | 次阅读

1、前言

在之前的一篇文章中Attention Mechanism综述讲述了Attention的背景和其应用场景，主要来自知乎的一篇精品博文摘抄。不过看完这篇博文只是对Attention的框架有了一个大概的了解，但是深入其里还是有些模糊。接下来本文就对Attention和Transformer进行更多细节上的探讨。

2、为什么Attention

一个新的结构或者模型出现都是为了解决某个问题的，目前的情况而言前馈网络和循环网络都有很强的能力,为什么还需要引入attention机制呢。

  • 计算能力的限制：当要记住很多“信息“，模型就要变得更复杂，然而目前计算能力依然是限制神经网络发展的瓶颈。
  • 优化算法的限制：虽然局部连接、权重共享以及pooling等优化操作可以让神经网络变得简单一些，有效缓解模型复杂度和表达能力之间的矛盾；但是，在循环神经网络中的长距离，信息“记忆”能力并不高。

Attention机制就是借助人脑处理信息方式：在处理某些信息的时候，对于输入的信息的注意力的分布会不一样，会容易去注意和目前目标有关的信息。

3、Attention机制分类

当用神经网络来处理大量的输入信息时，也可以借鉴人脑的注意力机制，只选择一些关键的信息输入进行处理，来提高神经网络的效率。按照认知神经学中的注意力，可以总体上分为两类：

  • 聚焦式（focus）注意力：自上而下的有意识的注意力，主动注意——是指有预定目的、依赖任务的、主动有意识地聚焦于某一对象的注意力；
  • 显著性（saliency-based）注意力：自下而上的有意识的注意力，被动注意——基于显著性的注意力是由外界刺激驱动的注意，不需要主动干预，也和任务无关；可以将max-pooling和门控（gating）机制来近似地看作是自下而上的基于显著性的注意力机制。

在人工神经网络中，注意力机制一般就特指聚焦式注意力。

4、Attention机制的计算流程

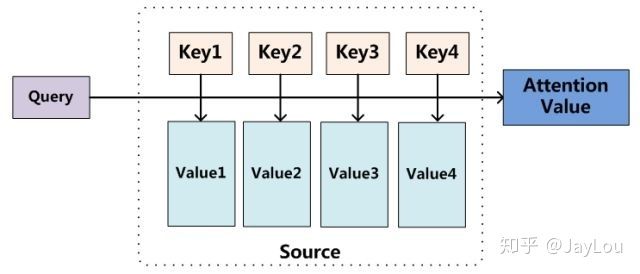
atttention机制计算流程

Attention机制的实质其实就是一个寻址（addressing）的过程，如上图所示：给定一个和任务相关的查询Query向量q，通过计算与Key的注意力分布并附加在Value上，从而计算Attention Value，这个过程实际上是Attention机制缓解神经网络模型复杂度的体现：不需要将所有的N个输入信息都输入到神经网络进行计算，只需要从X中选择一些和任务相关的信息输入给神经网络。

如上图所示，Attention机制大致可以分为三步：

  1. 信息输入：用$X=[x_1,x_2,…… ,x_N]$表示N 个输入信息
  2. 计算注意力分布$\alpha$:令$Key=Value=X$，则可以给出注意力分布:
    $$
    \alpha_i=softmax(s(key_{i},q))=softmax(s(X_{i},q))
    $$
  3. 根据注意力分布$\alpha$来计算输入信息的加权平均:注意力分布$\alpha_i$可以解释为在上下文查询q时，第i个信息受关注的程度，采用一种“软性”的信息选择机制对输入信息X进行编码为：
    $$
    att(q,X)=\sum_{i=1}^{N}{\alpha_i X_i}
    $$

在上面的计算流程中，我们将$\alpha_i$称之为注意力分布（概率分布），$s(X_i,q)$为注意力打分机制，有几种打分机制：

  • 加性模型：$s(X_i,q)=V^{T} tanh(WX_{i}+Uq)$
  • 点积模型：$s(X_i,q)=X^{T}_{i}q$
  • 缩放点积模型：$s(X_i,q)=\frac{X^{T}_{i}q}{\sqrt{d}}$
  • 双线性模型：：$s(X_i,q)=X^{T}_{i}Wq$

这种编码方式为 软性注意力机制（soft Attention），软性注意力机制有两种：普通模式(Key=Value=X) 和 键值对模式(Key！=Value)。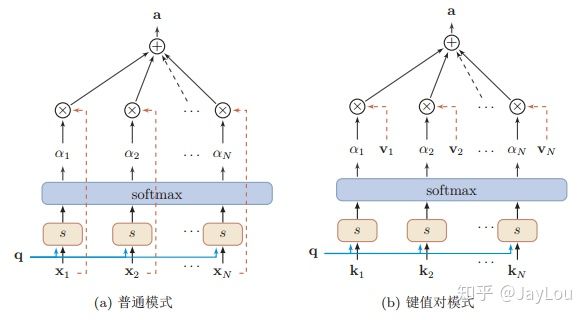
软性注意力机制（soft Attention）

4.1 self attention计算流程

因为Attention实现的方式有很多种，我们难以每种都介绍，下面我们就介绍最基础和常见的Multi-Head Attention 与 Scaled Dot-Product Attention。
Multi-Head Attention和Scaled Dot-Product Attention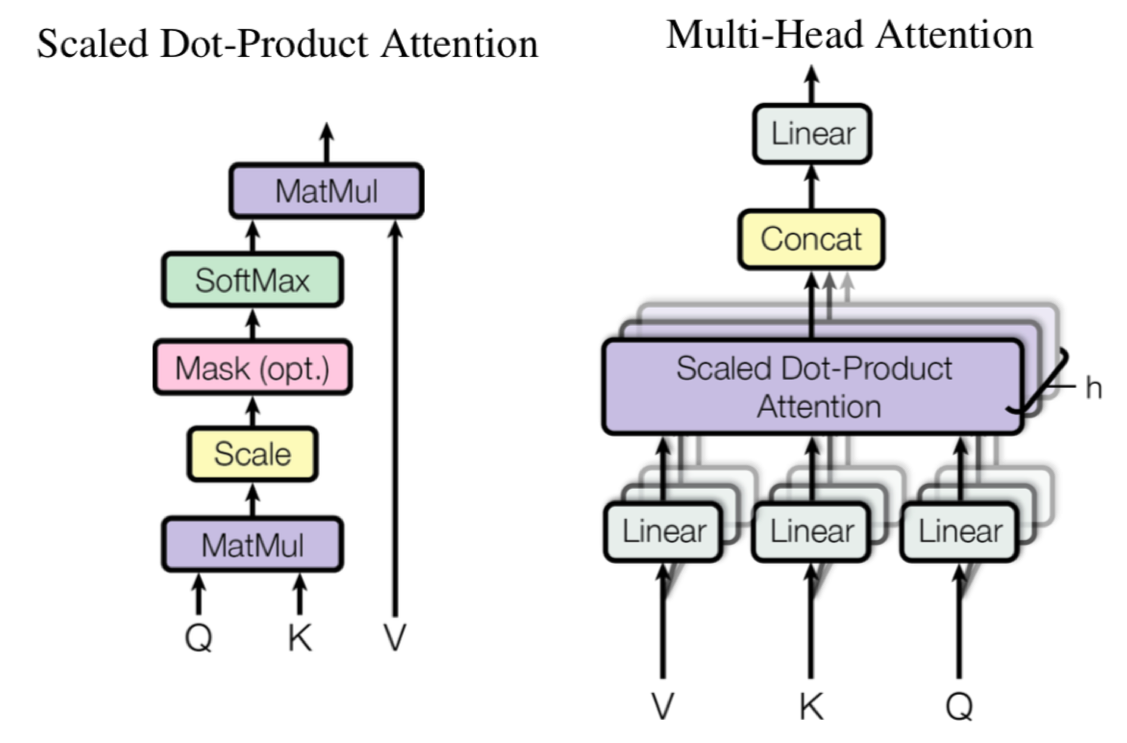
首先我们介绍Scaled Dot-Product Attention，如果要先理解Scaled Dot-Product Attention我们必须先理解Q、K、V从哪来。以下计算步骤我们先使用self-attention的计算过程来帮助大家理解attention的计算过程。
第一步 就是将输入的X通过转换矩阵对输入的X做线性转换后转换为Q、K、V。如下图所示: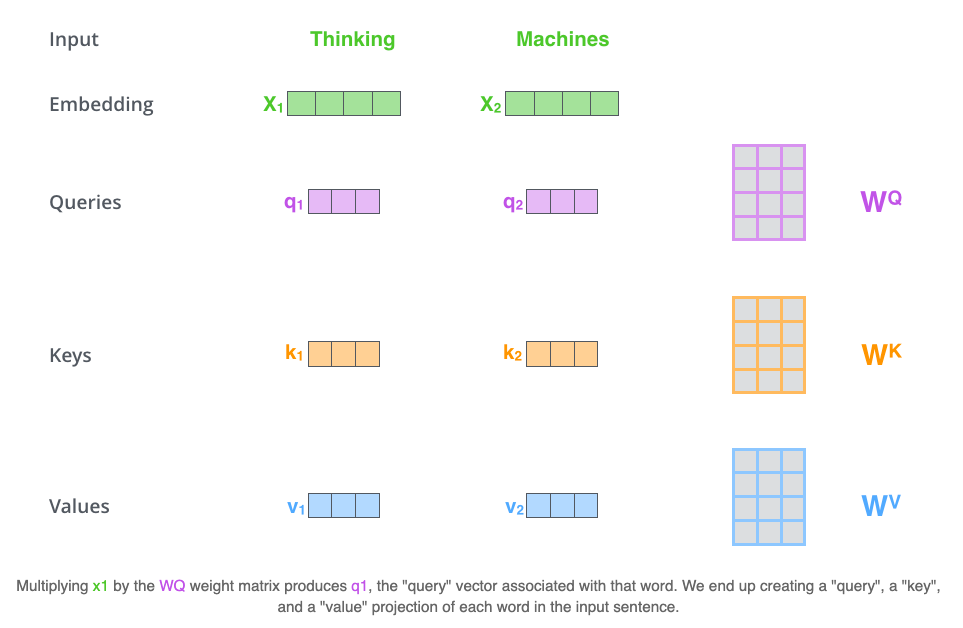
Self Attention的KQV计算
从上图中可以看出输入$X_{1}$与转换矩阵$W^{Q}$相乘之后的到$q_{1}$,同理我们经过矩阵$W^{K}$和$W^{V}$得到$k_{1}$和$v_{1}$。
对于计算出来的query, key以及value向量他们对于理解attention的计算机制很有帮助，且attention接下来的计算机制都需要依赖这几个向量。
第二步 接下来就是一句第一步算好的q、k、v向量计算score。我们以上述例子中首个单词‘thinking’的计算过程如下：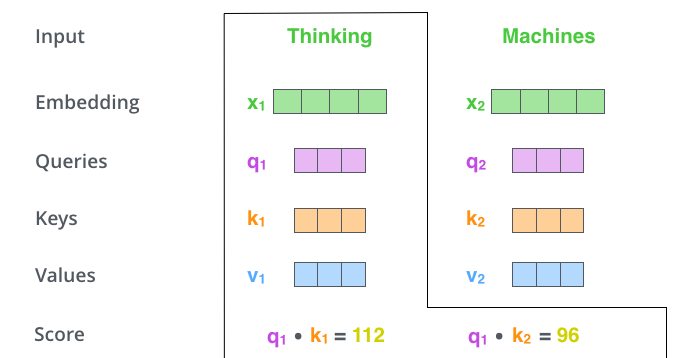
Self Attention Score
score是由query vector和key vector相乘而得来，$score_{1}$是由$k_{1}$和$v_{1}$计算而来，$score_{2}$是由$k_{2}$和$v_{2}$计算而来,’thinking’会依次和所有的输入序列算一个score值，计算方式与$score_{1}$、$score_{2}$一致。
第三步及第四步 我们将得到的结果除以8(key vectors的维数的平方根，论文中解释是为了得到更加稳定的梯度),然后将得到的结果输入到softmax进行归一化使得输出的结果相加后为1。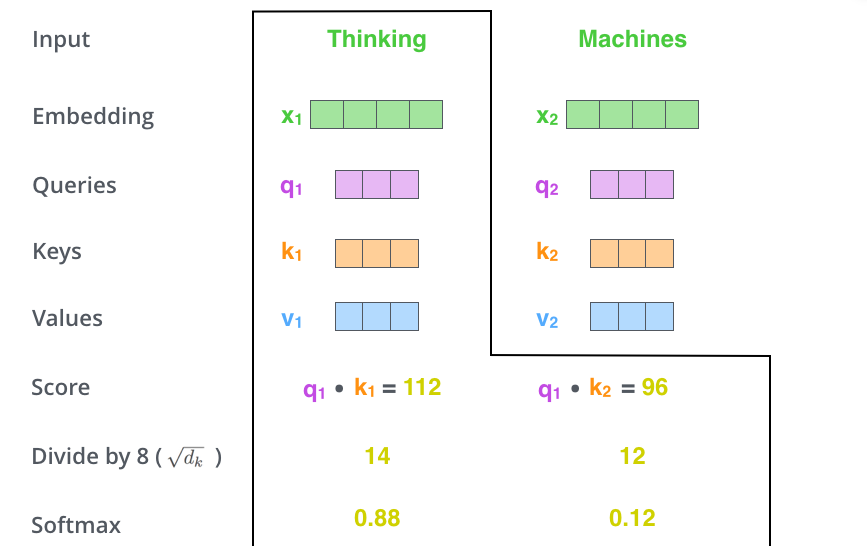
Self Attention softmax
softmax输出的socre会算出序列中每个单词与当前计算序列点的贡献度，有时其他单词对当前单词的翻译结果还是很重要的。
第五步 将softmax socre与value vertor相乘，这里目的是为了让我们关注的单词尽量保持不变，并忽略掉我们不关注的单词的值(比如socre值很小，乘以晓得值后值会变得很小)。
第六步 对加权后的value vector进行求和得到$Z$,这一步的目的是为了获取当前序列点的输出。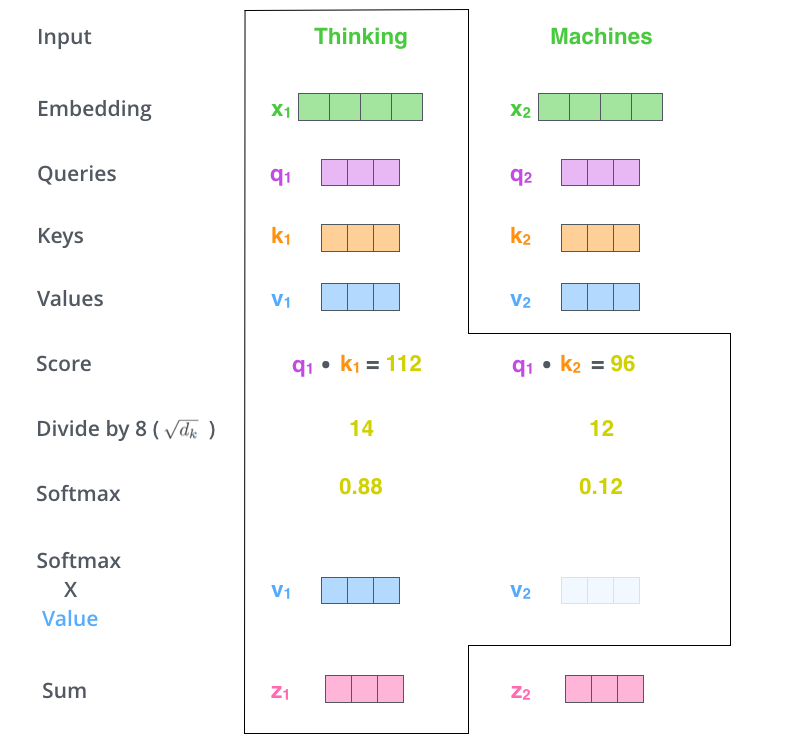
Self Attention output
以上我们介绍了self attention是如何具体计算的，接下来我们看看self attention的矩阵计算方式。
第一步 计算出Query, Key, Value矩阵，如下所示: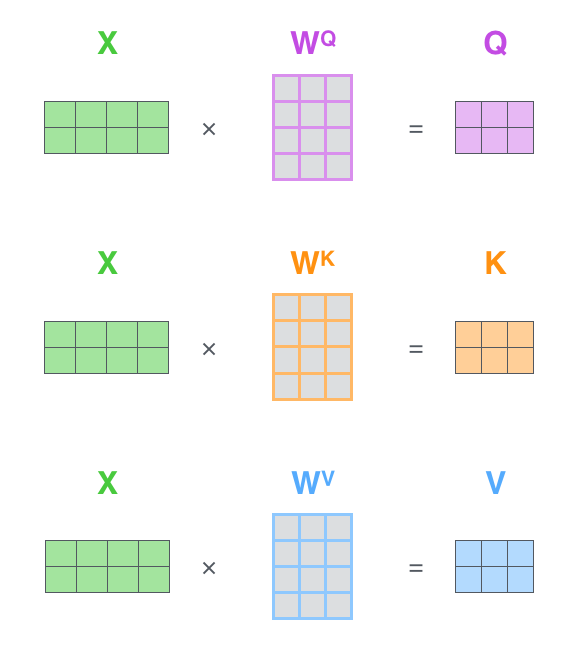
Self Attention matrix caculate 01
输入是一个[2x4]的矩阵（单词嵌入），每个运算是[4x3]的矩阵，求得Q,K,V。
第二步 计算attention的输出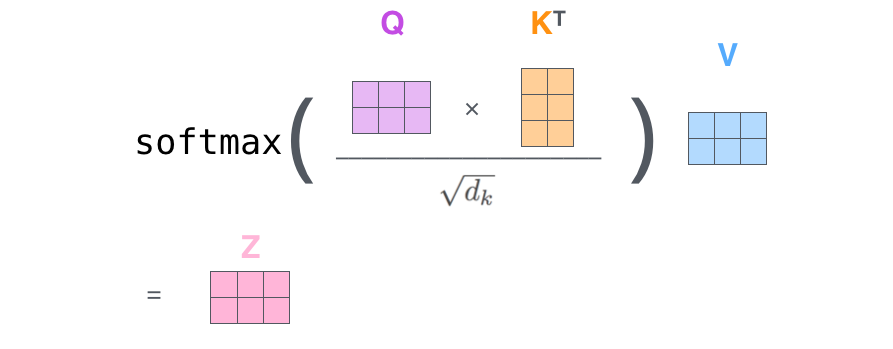
Self Attention matrix caculate 02
Q对K转置做点乘，除以$d_k$的平方根。做一个softmax得到合为1的比例，对V做点乘得到输出Z。那么这个Z就是一个考虑过thinking周围单词的输出。
依据以上得出结果:
$$Attention=softmax(\frac{QK^{T}}{\sqrt{d_{k}}})V$$
以上公式中$QK^{T}$其实会构成一个word2word的attention map，在加入了softmax后只是将数值进行了归一化处理。如下图所示翻译任务中的attention矩阵: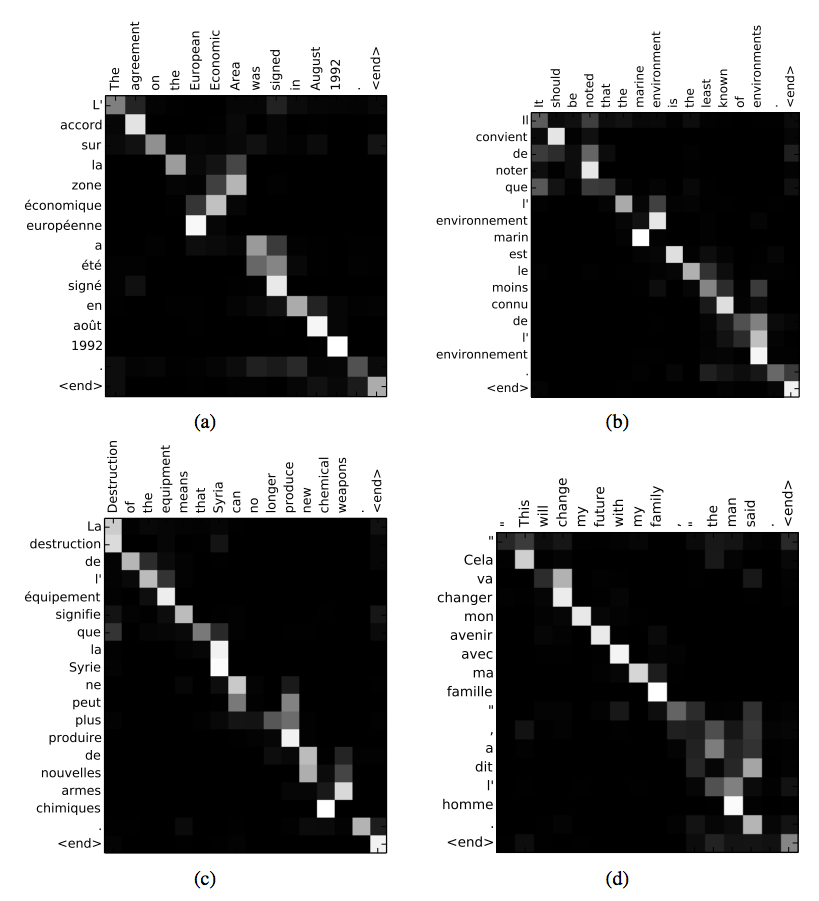
Self Attention matrix
self-attention这里就出现一个问题，如果输入的句子特别长，那就为形成一个 NxN的attention map，这就会导致内存爆炸…所以要么减少batch size多gpu训练，要么剪断输入的长度，还有一个方法是用conv对K,V做卷积减少长度。

4.2 Multi-Head Attention计算流程

在 Multi-Head Attention中，我们为每一个头部保持单独的q/k/v权重矩阵，从而得到不同的q/k/v矩阵。如前所述，我们将$X$乘以$W^{Q}//W^{K}/W^{V}$矩阵，得到q/k/v矩阵。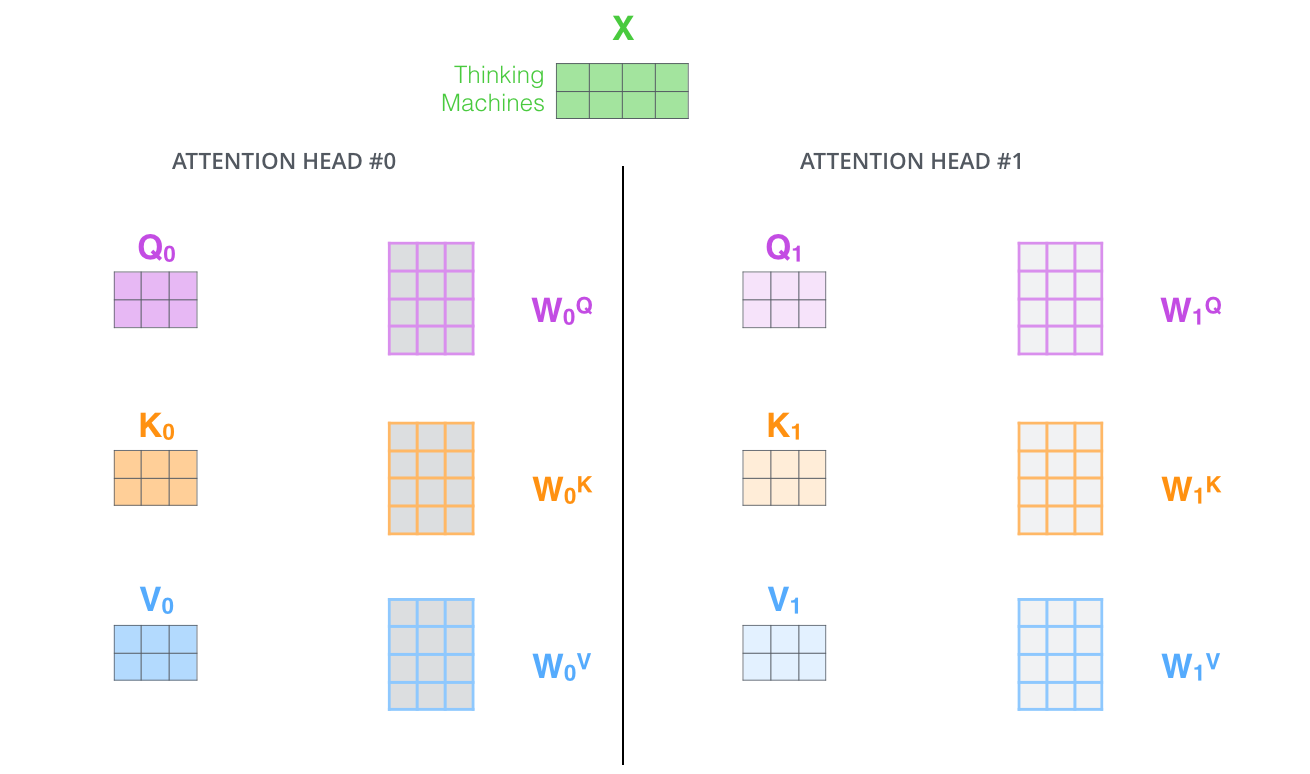
Multi-Head Attention heads
由接下来我们可以算出不同head得到的不同的输出$Z_{0},Z_{1},Z_{2},…,Z_{7}$,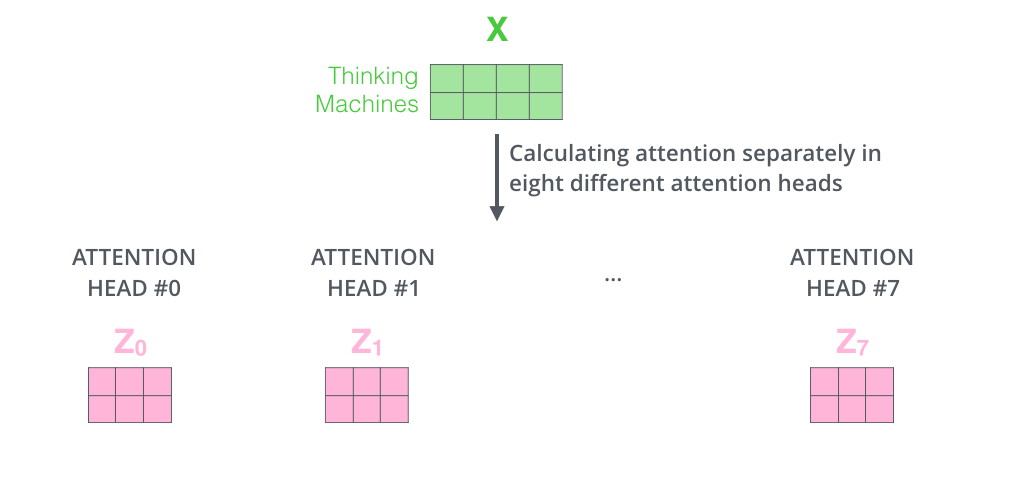
Multi-Head Attention outputs
我们得到不同head的输出后，将结果进行拼接(concatenate),然后将得到拼接后的$\hat{Z}$与矩阵$W^{0}$进行点乘得到最终输出Z。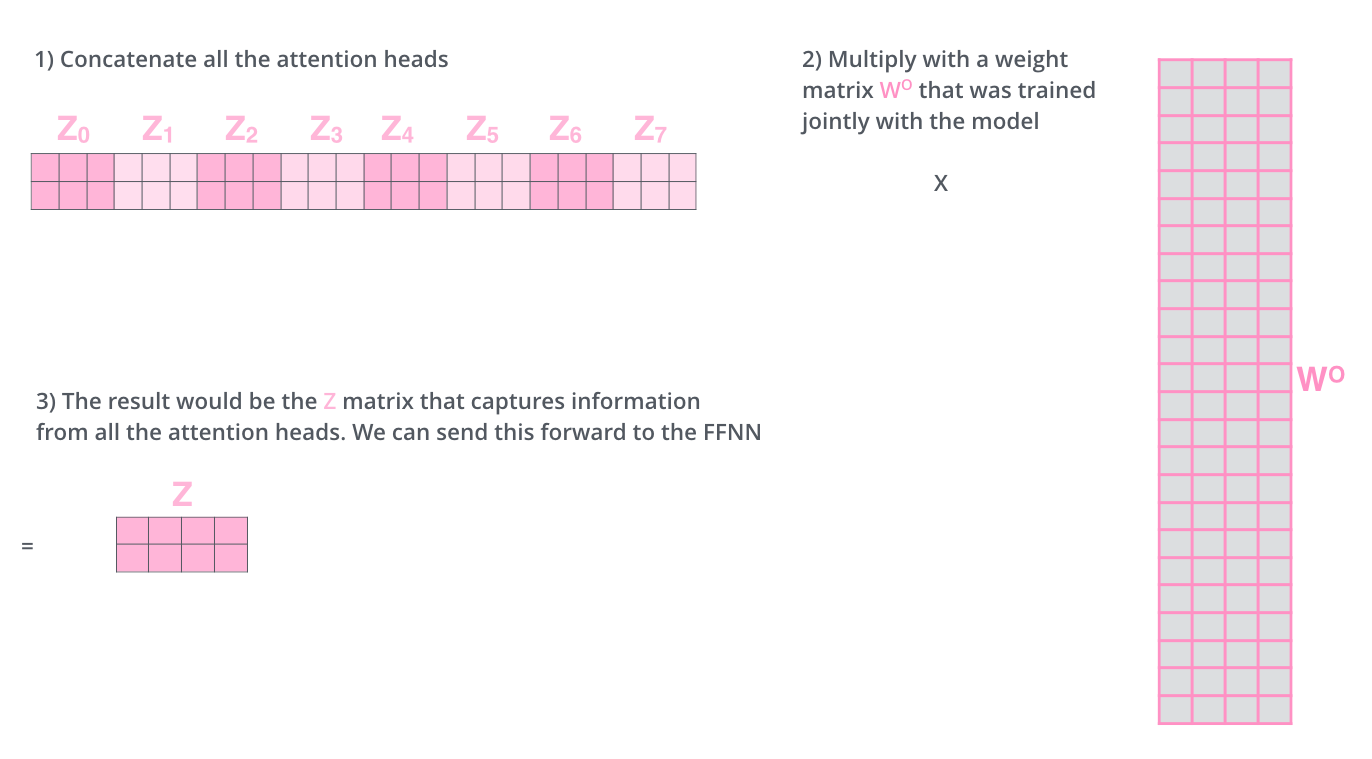
Multi-Head Attention outputs concat
Multi-Head Attention整个过程如下如所示: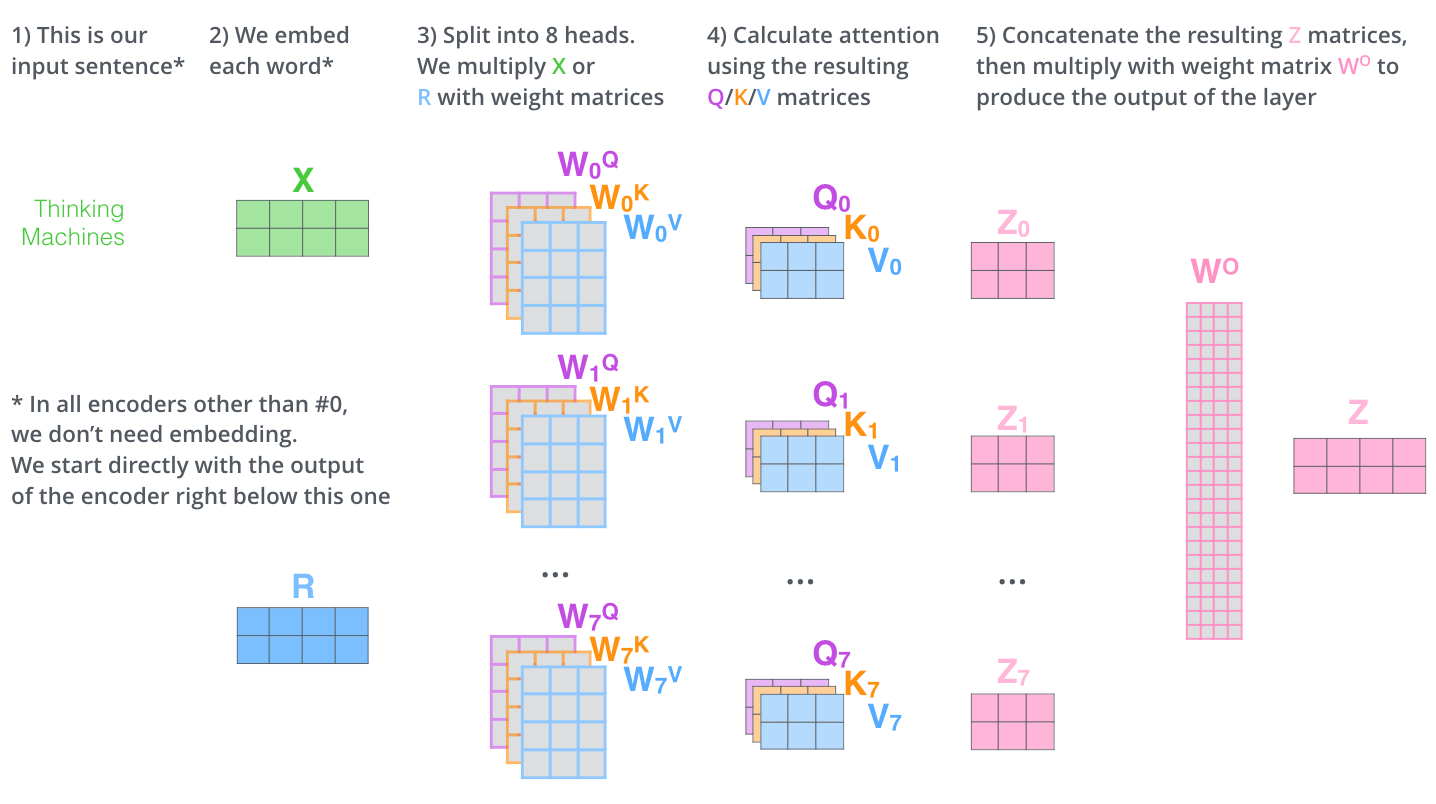
Multi-Head Attention计算流程

5、Transformer框架

Transformer是谷歌在17年做机器翻译任务的“Attention is all you need”的论文中提出的，引起了相当大的反响。在“Attention is all you need”论文中说的Transformer指的是完整的Encoder-Decoder框架，如下图所示: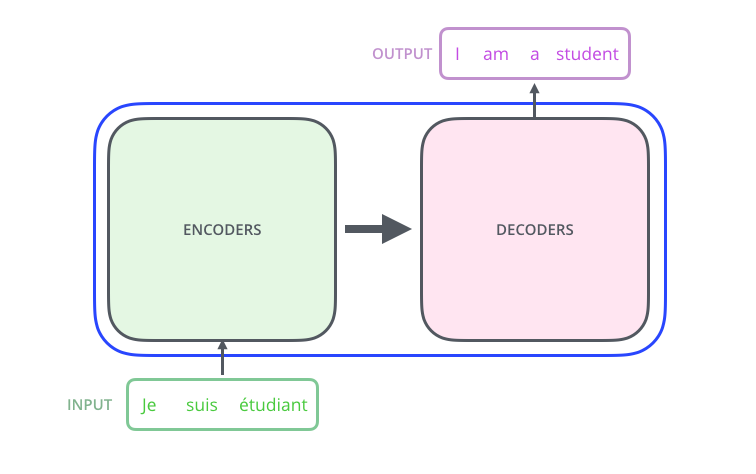
transformer整体框架
在Encoders部分是由若干个Encoder单元组成，Dencoders部分是由若干个Decoder单元组成，其展开结构如下所示: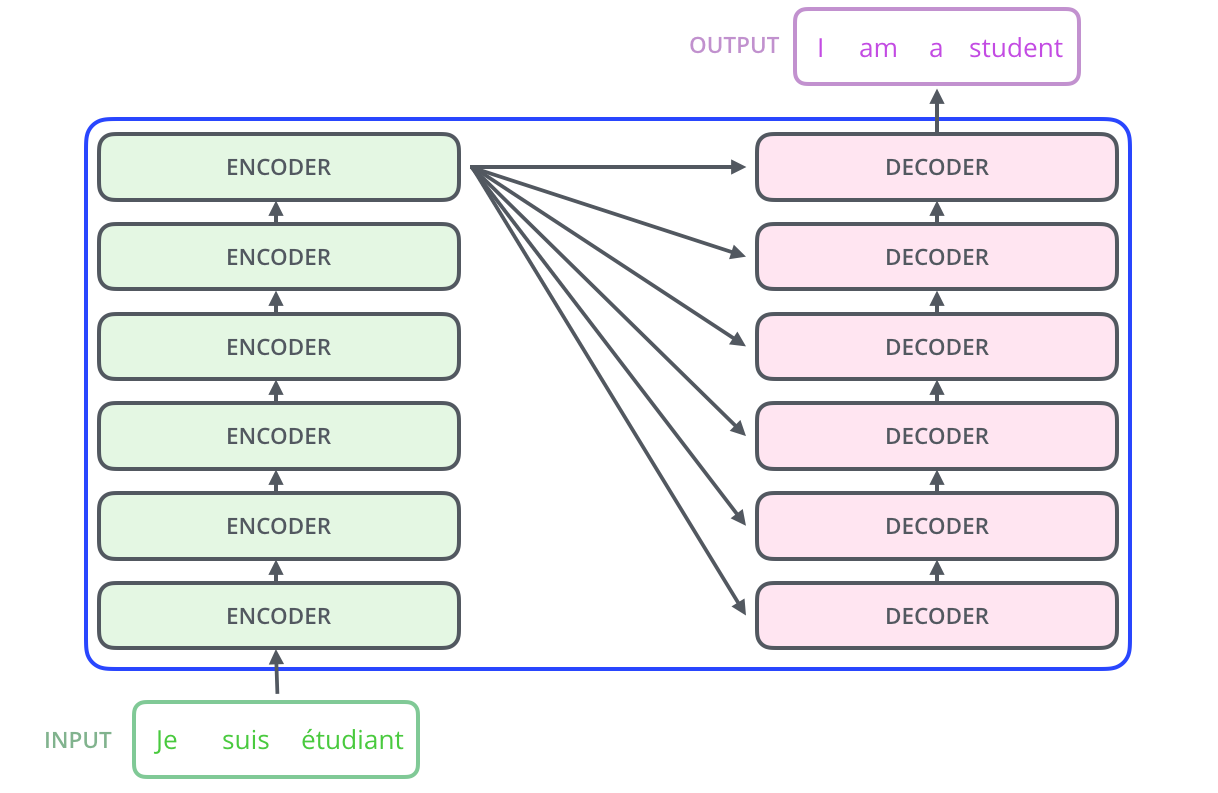
transformer整体框架展开部分

5.1 Encoder单元

然后我们在针对以上的Ender单元在继续展开，发现Encoder部分主要是由self-attention部分和前馈神经网络构成，如下图所示: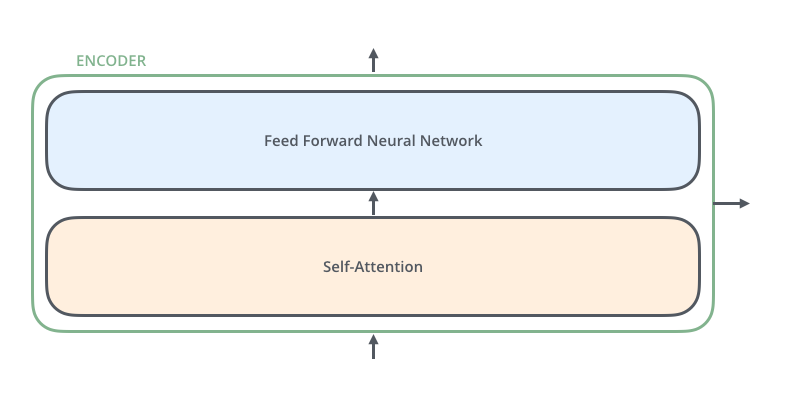
transformer Encoder 单元01
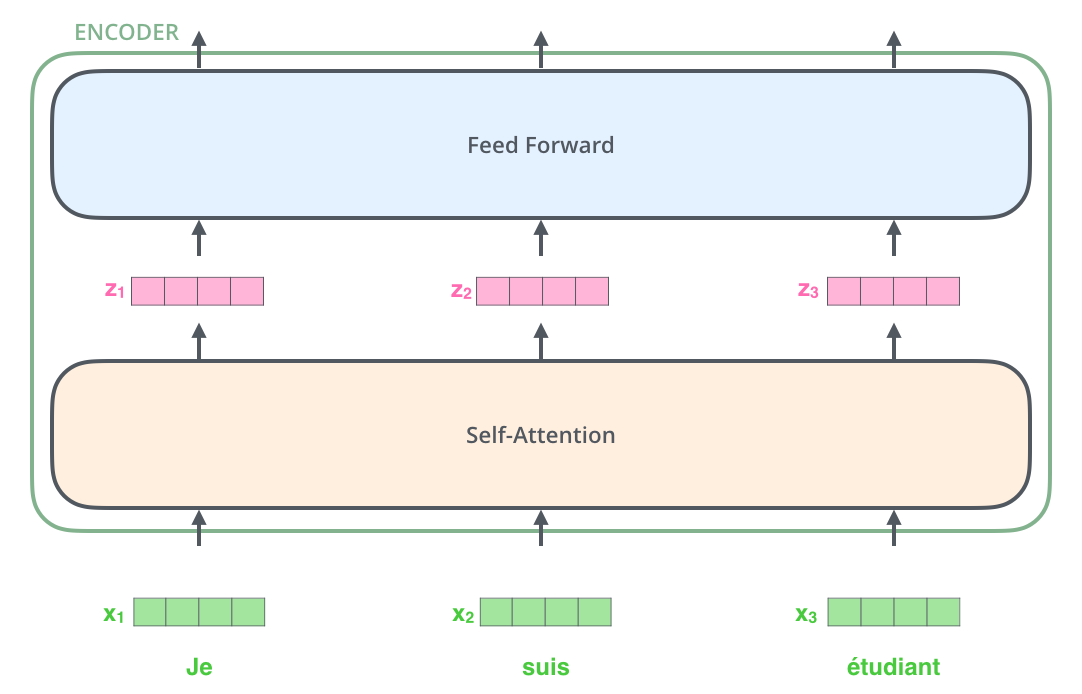
transformer Encoder 单元02
通过self-attention得到$Z$后，它会被送到encoder的下一个模块，即Feed Forward Neural Network。这个全连接有两层，第一层的激活函数是ReLU，第二层是一个线性激活函数，可以表示为：
$$FFN(Z)=max(0,ZW_{1}+b_{1})W_{2}+b_{2}$$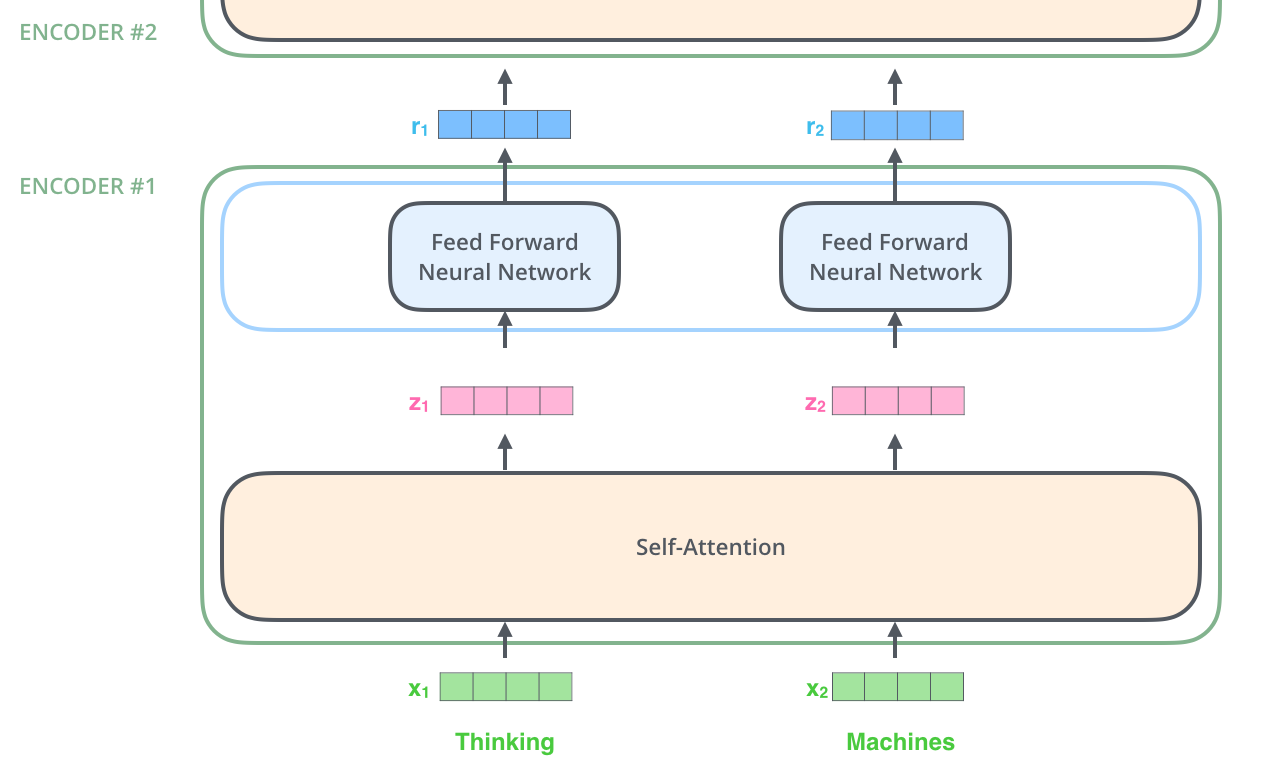
transformer Encoder 单元03
Transformer框架因为为了解决深度网络带来的退化问题，引入了残差网络部分(Residuals)如下所示: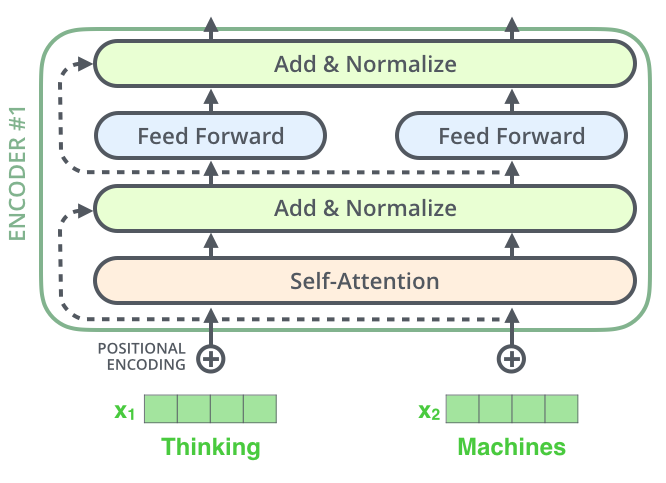
transformer Residuals
我们展开layer-norm看的更细致，如下图所示：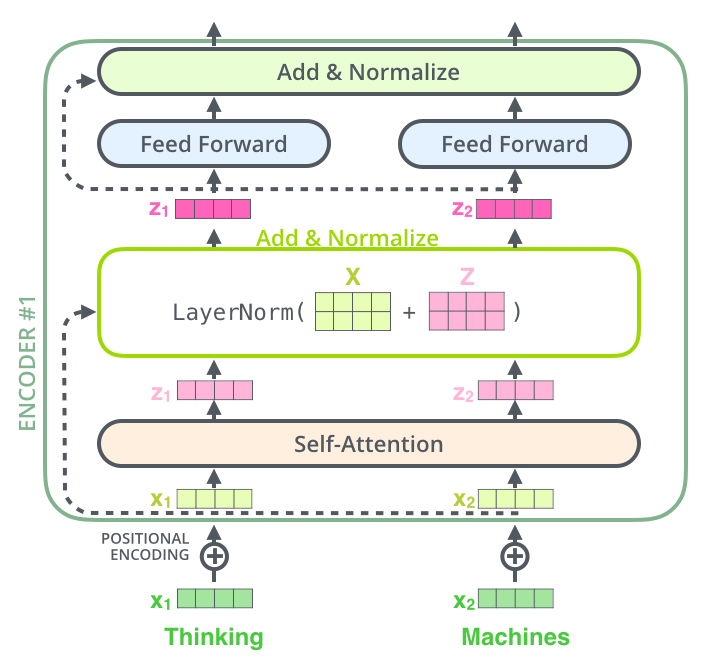
transformer layer-norm
从上面我们可以看到还有一个positition embedding没有介绍。在transformer机制中加入位置信息主要是为了增加捕捉顺序序列的能力，如果不加入位置信息那么就是说无论句子的结构怎么打乱，Transformer都会得到类似的结果。换句话说，Transformer只是一个功能更强大的词袋模型而已。
为了解决这个问题，论文中在编码词向量时引入了位置编码（Position Embedding）的特征。具体地说，位置编码会在词向量中加入了单词的位置信息，这样Transformer就能区分不同位置的单词了。
那么怎么编码这个位置信息呢？常见的模式有：a. 根据数据学习；b. 自己设计编码规则。在这里作者采用了第二种方式。那么这个位置编码该是什么样子呢？通常位置编码是一个长度为 [公式] 的特征向量，这样便于和词向量进行单位加的操作,如下图所示: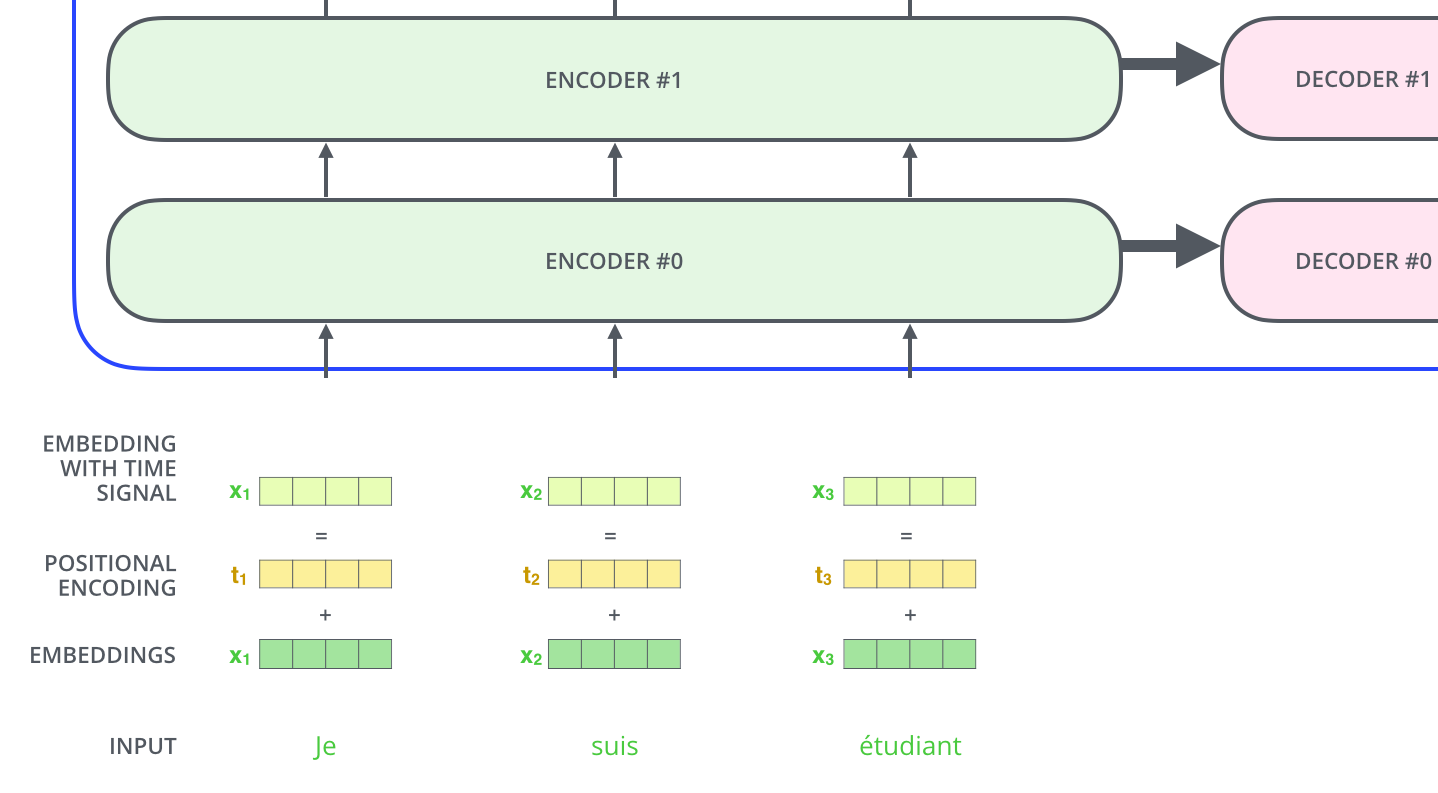
transformer position embeding
论文给出的编码公式如下：
$$
PE(pos,2i)=sin(\frac{pos}{10000^{\frac{2i}{d_{model}}}})\\
PE(pos,2i+1)=cos(\frac{pos}{10000^{\frac{2i}{d_{model}}}})
$$
在上式中，$pos$表示单词的位置，意为 token 在句中的位置，设句子长度为 L ，则$pos=0,1,2,3,….,L-1$;$i$表示向量的某一维度,若$d_{model}=512$时，$i=0,1,…,255$.作者这么设计的原因是考虑到在NLP任务重，除了单词的绝对位置，单词的相对位置也非常重要。根据公式$sin(\alpha+\beta)=sin\alpha cos\beta+cos\alpha sin\beta$及$cos(\alpha+\beta)=cos\alpha cos\beta-sin\alpha sin\beta$，这表明位置$k+p$的位置向量可以表示为位置$k$的特征向量的线性变化，这为模型捕捉单词之间的相对位置关系提供了非常大的便利。
我们假设embedding大小为4，那么其真实的positional encodings如下所示: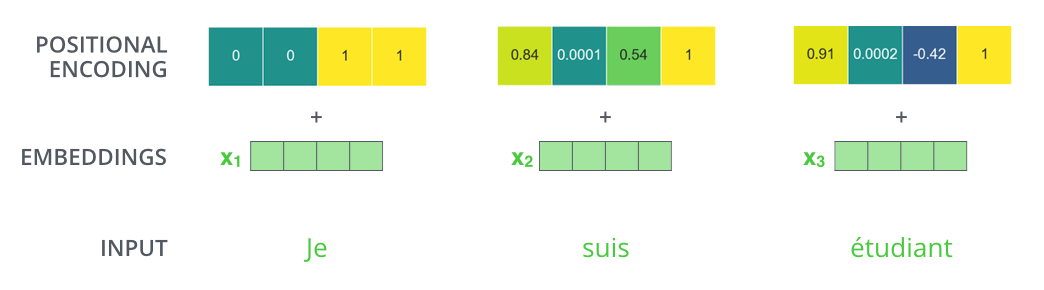
transformer position embeding

5.2 Decoder单元

然后我们把Decoder单元展开，发现Decoder部分和Encoder部分非常接近，但是多了一个Encoder-Decoder Attention单元，如下所示: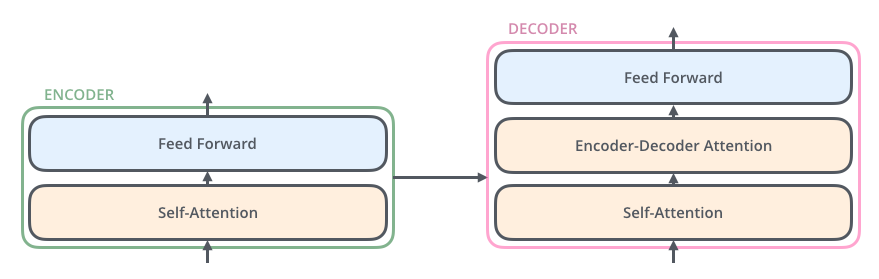
transformer Decoder 单元
Decnoder单元中的两个Attention分别用于计算输入和输出的权值：

  • Self-Attention：当前翻译和已经翻译的前文之间的关系；
  • Encoder-Decnoder Attention：当前翻译和编码的特征向量之间的关系。

在encoder-decoder attention中， $Q$来自于解码器的上一个输出，$K$和$V$则来自于与编码器的输出,计算方式和self attention的计算方式是一致的。
其中$K$和$V$的转换过程如下: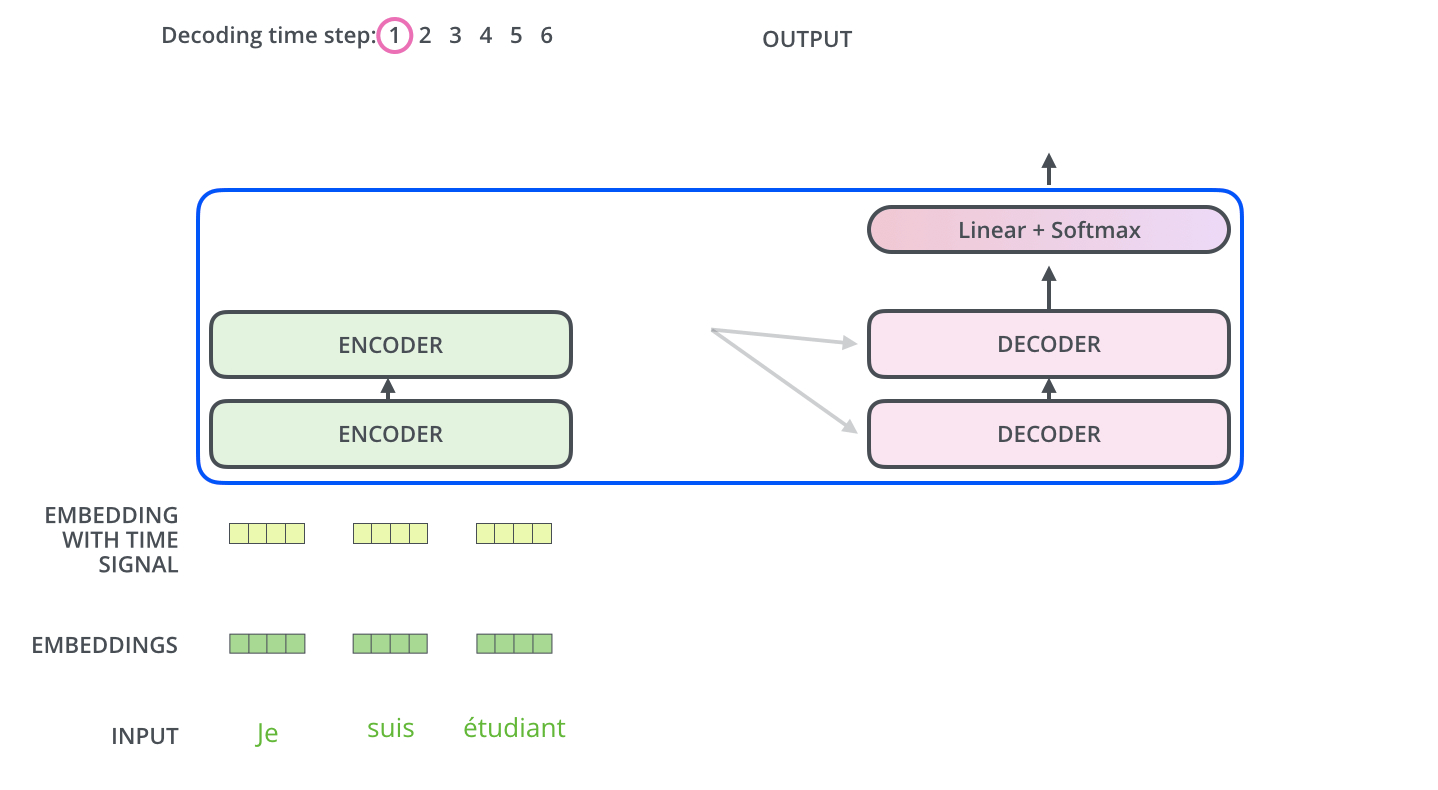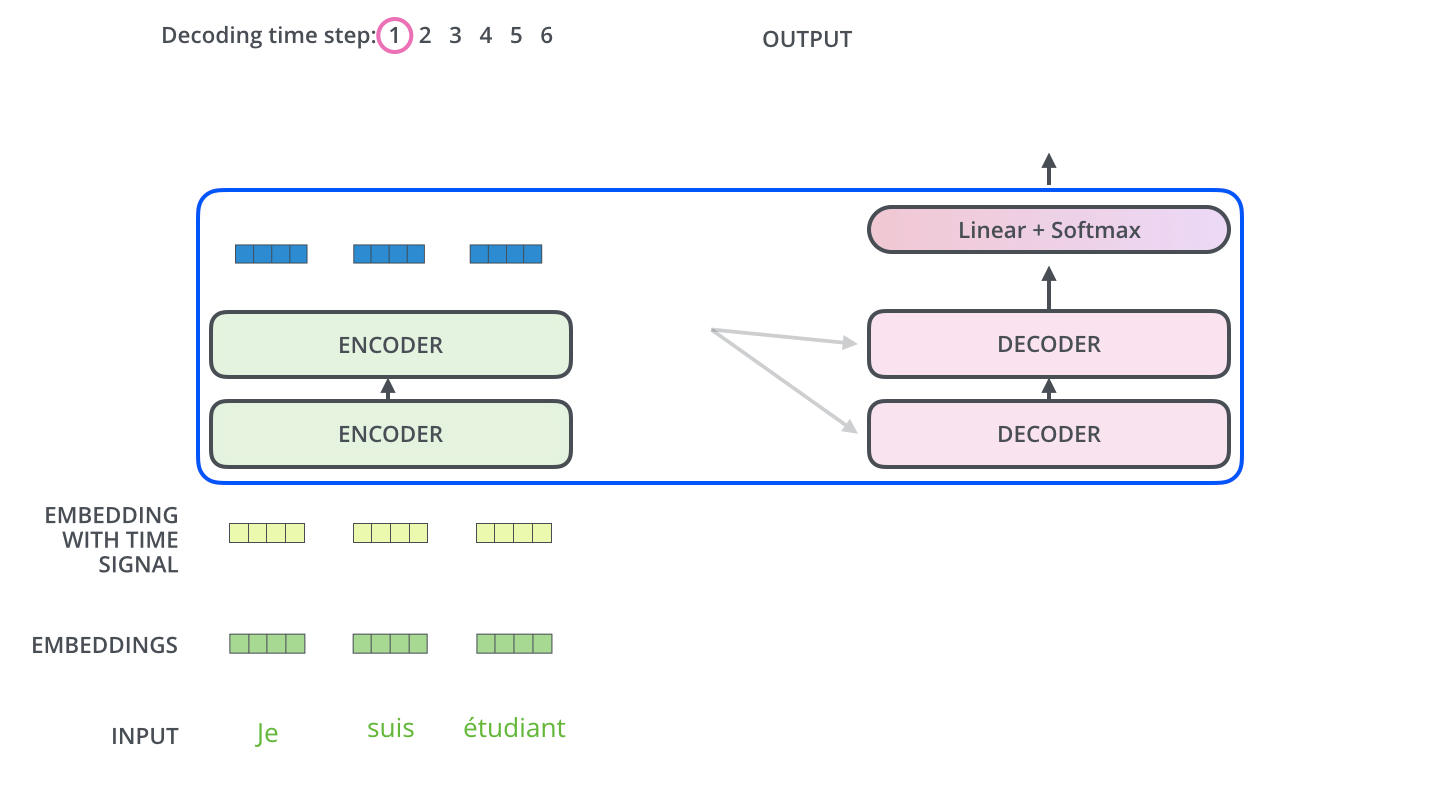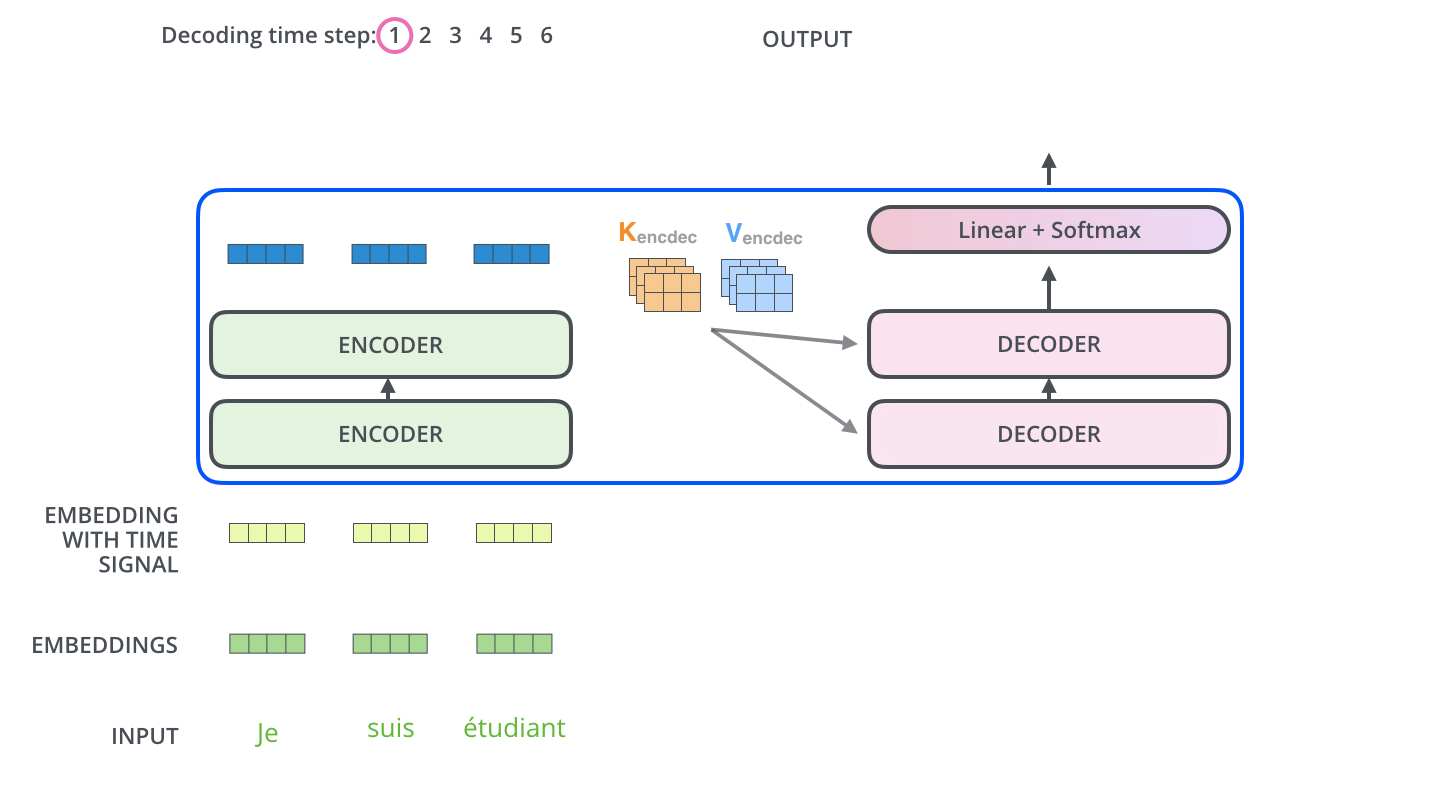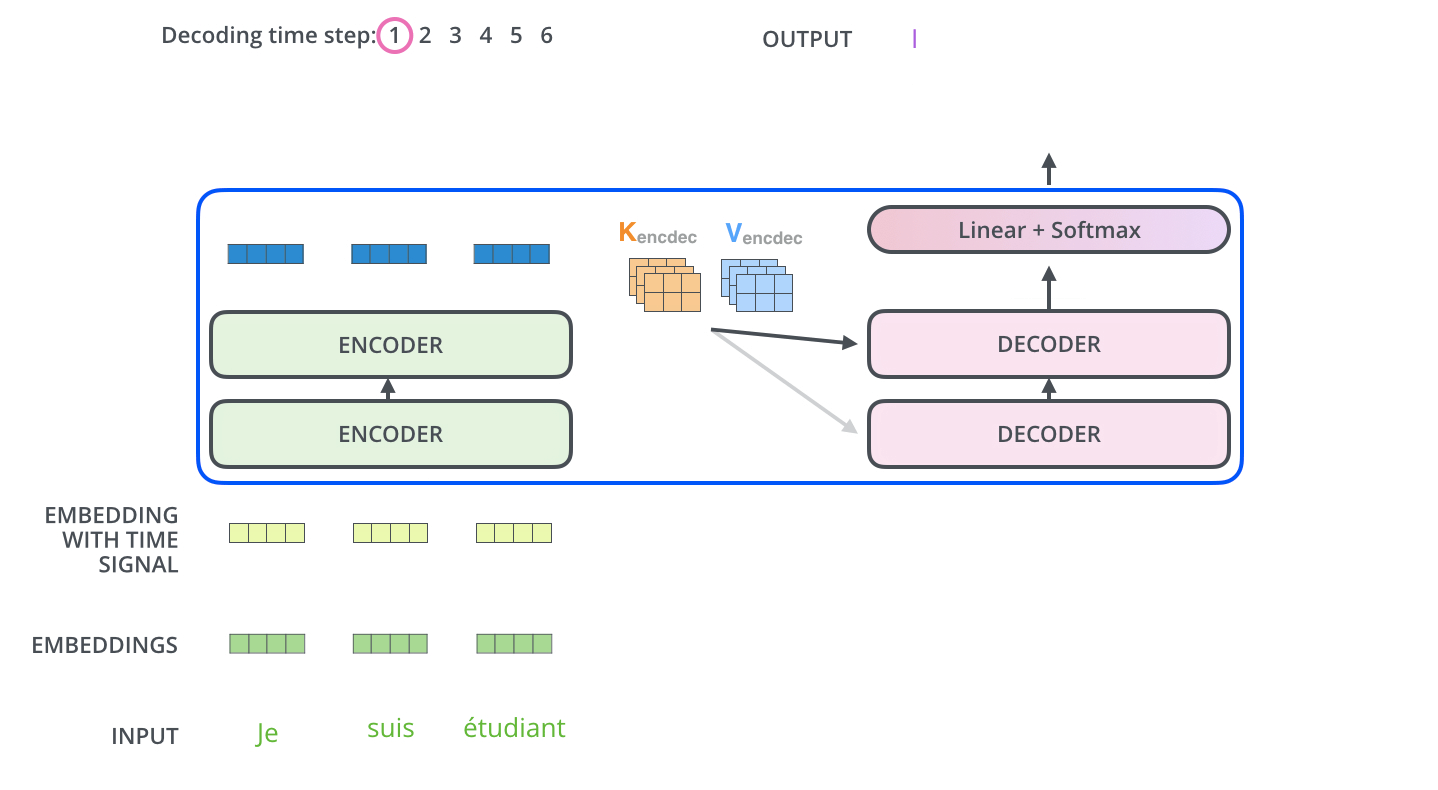
transformer decoder计算KV
encoder-decoder attention有助于解码器聚焦在对当前解码器有用的输入序列位置上。
上面展示了编码器到解码器的过程，接下来我们展示解码器逐步解码的过程，如下图: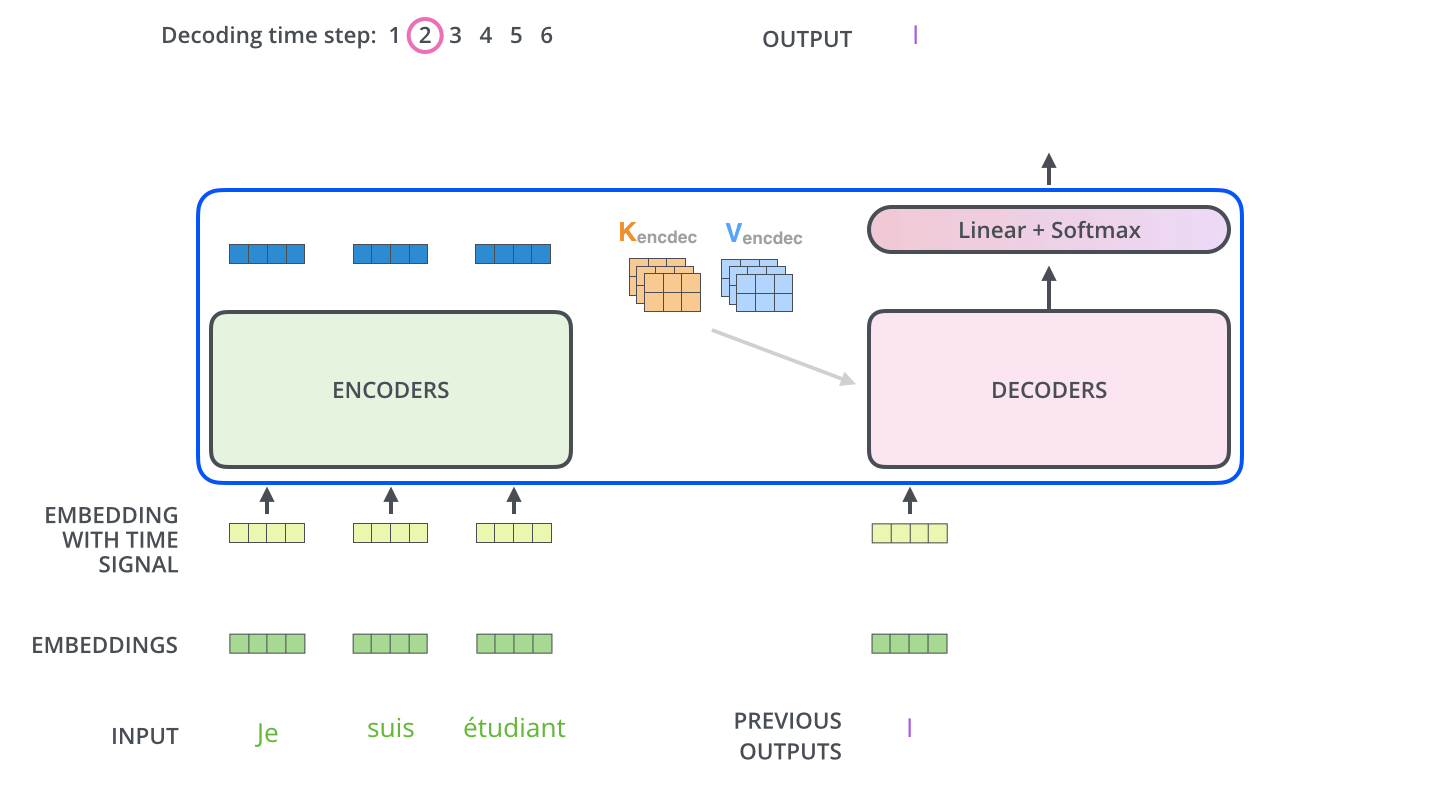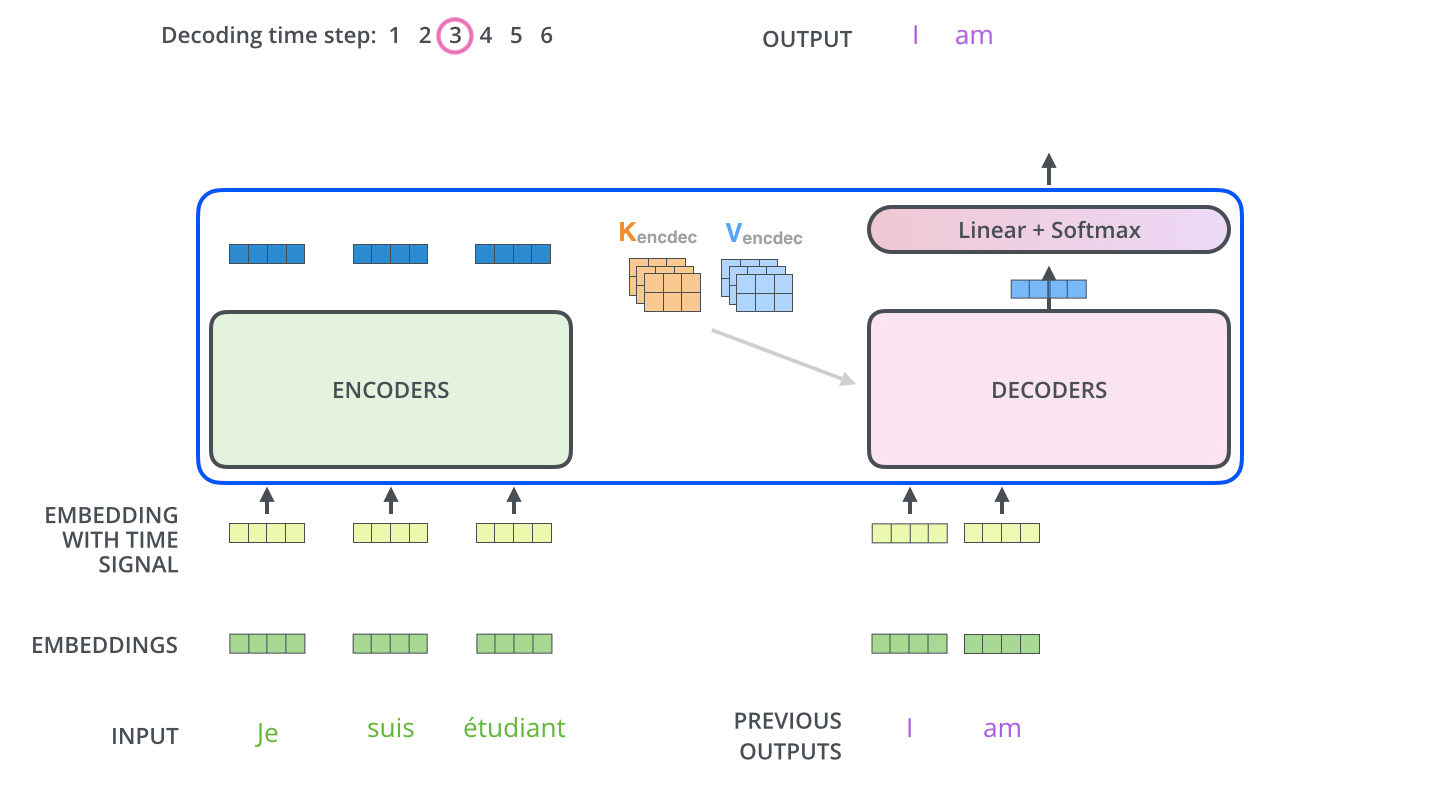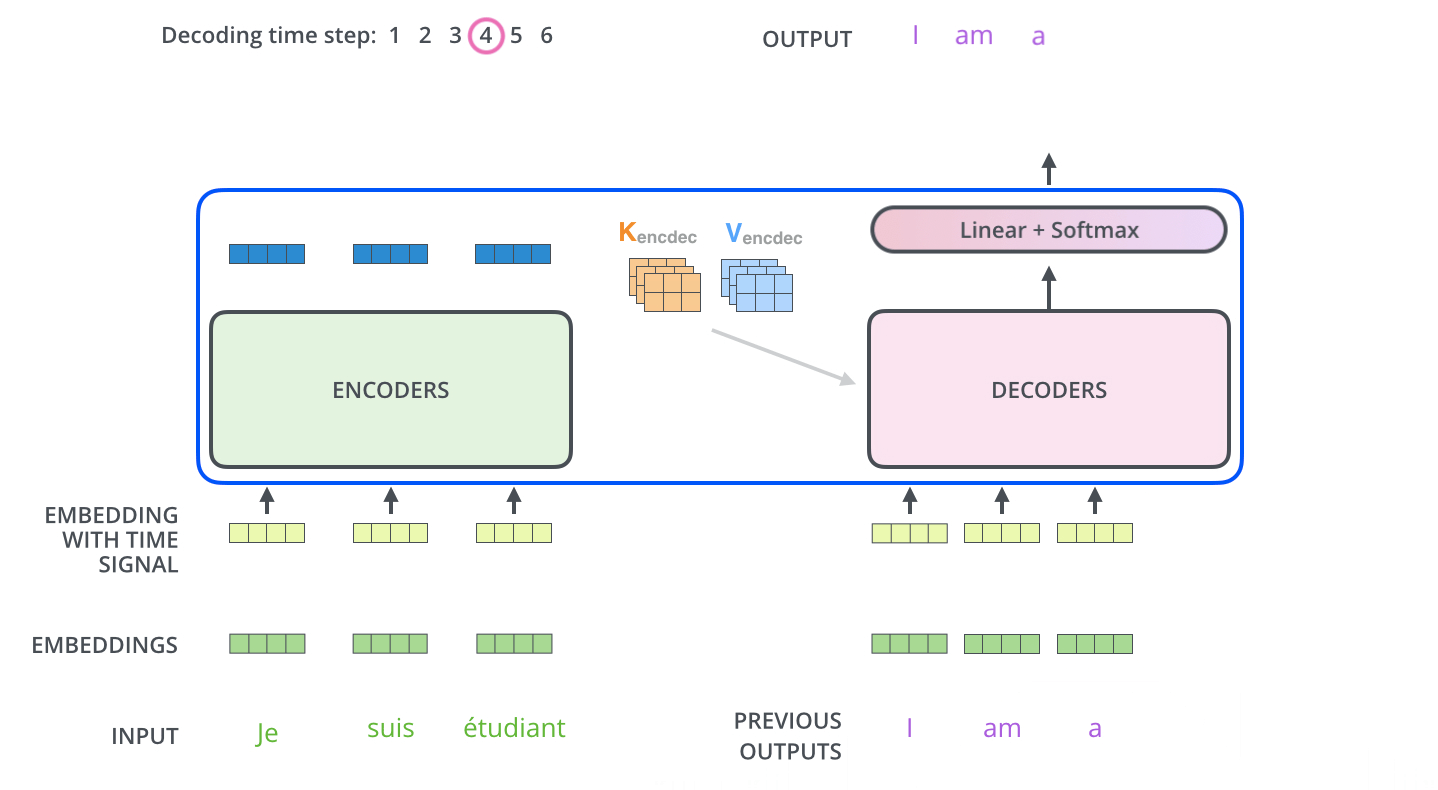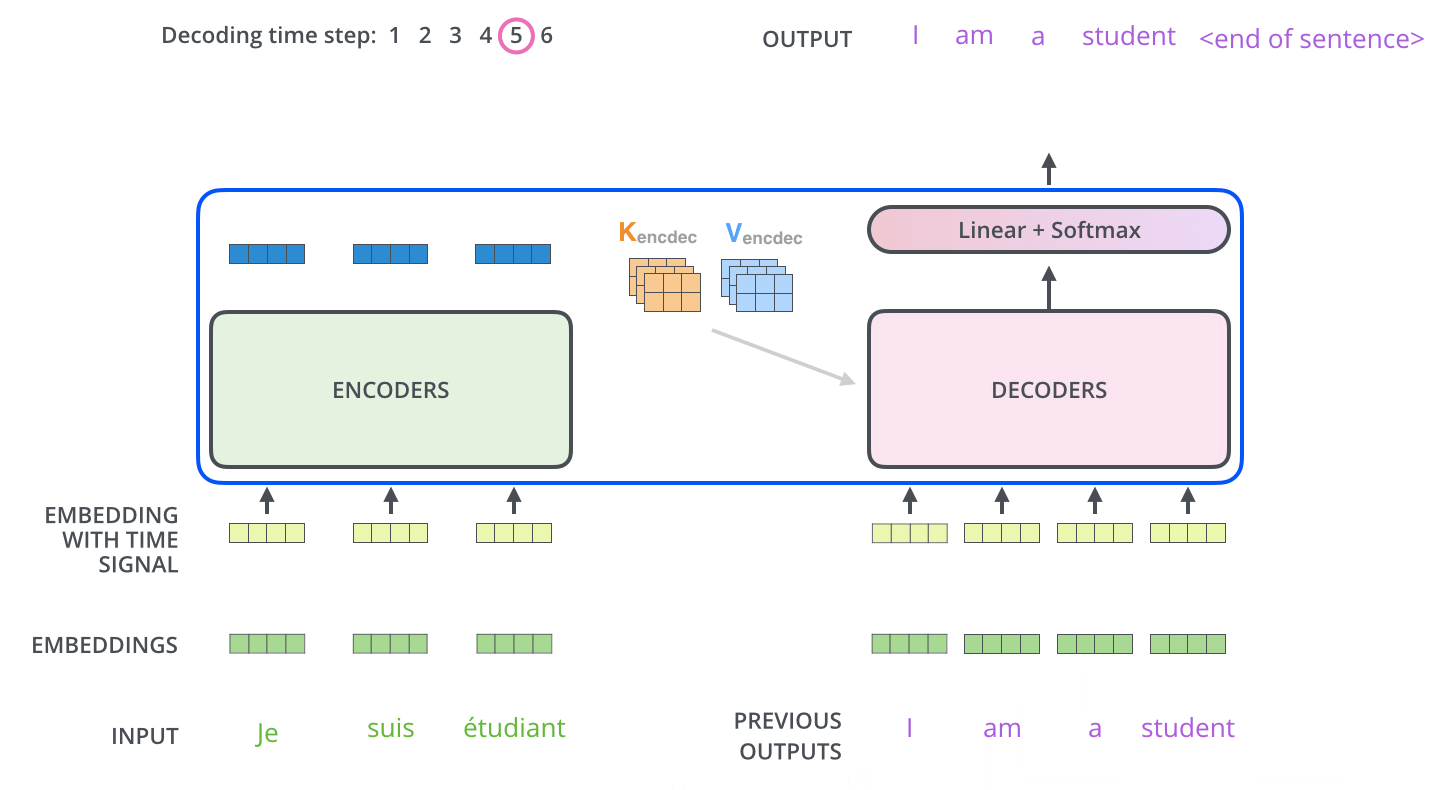
transformer decoder逐步解码
以上步骤一直重复知道到结束符号为止，每一步的输出在下一个时间被输入到底层解码器，解码器输出结果和编码器是一样的，只是解码器是逐个输出。我们在解码器输入中嵌入并添加位置编码来指示每个单词的位置，这点和编码器的做法是一致的。

5.3 损失层

解码器解码之后，解码的特征向量经过一层激活函数为softmax的全连接层之后得到反映每个单词概率的输出向量。此时我们便可以通过CTC等损失函数训练模型了。
而一个完整可训练的网络结构便是encoder和decoder的堆叠(各N个)。我们可以得到transformer的整体结构如下图所示: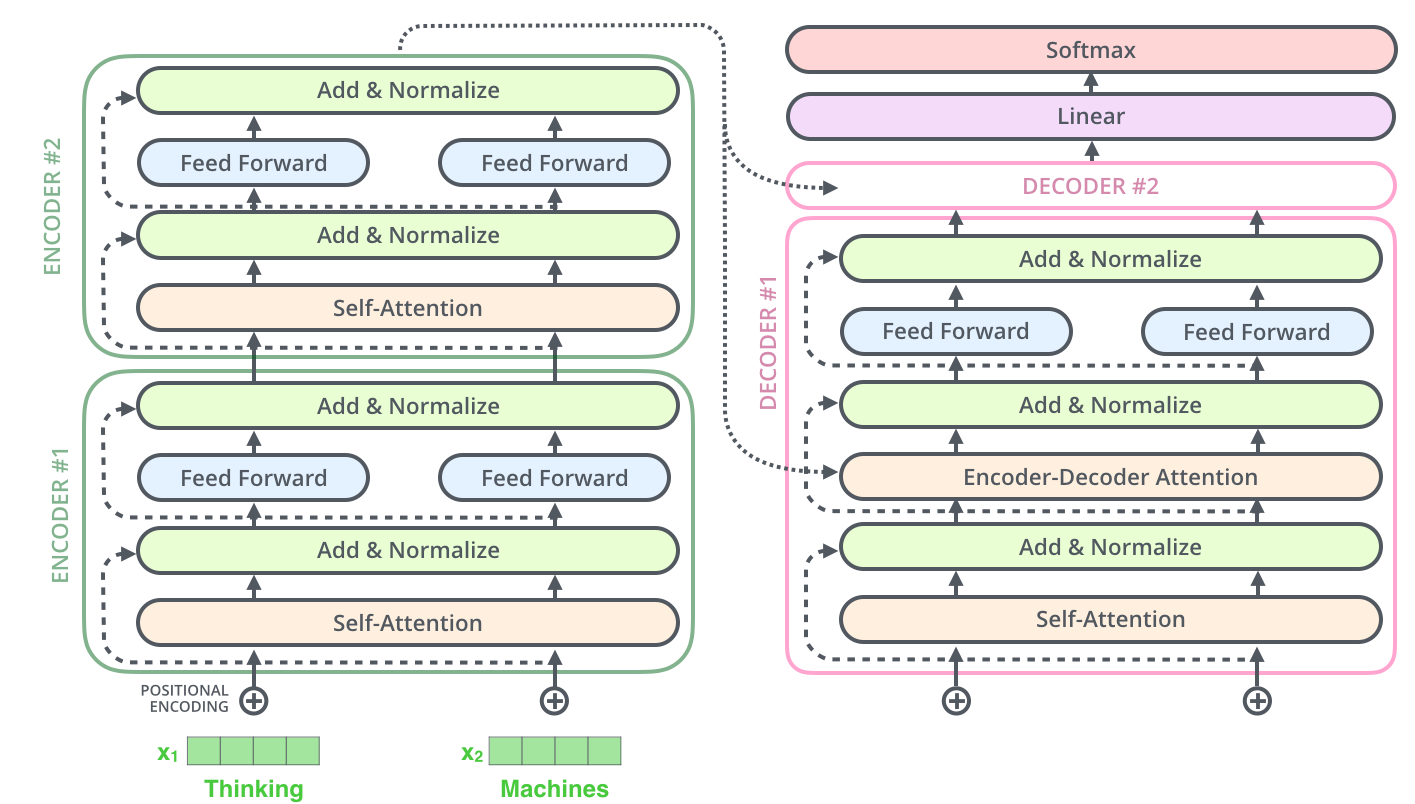
transformer position embeding

6、总结

通过上文的分析其实我们能够对Attention和Transformer有个很清晰地了解了，从我个人的理解而言这两个都不是某一个固定的模型，而是一个思想框架，所以其实现有很多种即有很多变种，类似RNN中的LSTM、GRU等等。Transformer中Attention是其很重要的一个单元，在加上位置信息来捕捉时序信息，其主要承担了RNN部分的功能。而Transformer依然使用的是Encoder-Decoder框架，只是在Encoder和Decoder部分的单元做了设计和构思。Transformer的设计最大的带来性能提升的关键是将任意两个单词的距离是1，这对解决NLP中棘手的长期依赖问题是非常有效的。Transformer不仅仅可以应用在NLP的机器翻译领域，甚至可以不局限于NLP领域，是非常有科研潜力的一个方向，同时算法的并行性非常好，符合目前的硬件（主要指GPU）环境。
但是Transformer并非没有缺点的，粗暴的抛弃RNN和CNN虽然非常炫技，但是它也使模型丧失了捕捉局部特征的能力;Transformer失去的位置信息其实在NLP中非常重要，而论文中在特征向量中加入Position Embedding也只是一个权宜之计，并没有改变Transformer结构上的固有缺陷。

参考