一、简介

条件随机场模型是Lafferty等人在2001年在最大熵模型和隐马尔可夫模型的基础上提出的一种无向图模型，是一种基于标注和切分有序数据的条件概率模型。
CRF最早是针对序列数据分析提出的，现已成功应用于自然语言处理、生物信息学、机器视觉及网络智能等领域。目前基于CRF的实现有CRF,FlexCRF,CRF++。

二、预备知识

条件随机场比较复杂，因此也涉及到很多前置的预备知识:概率图模型、马尔可夫性、团与最大团等。

2.1、概率图模型(PGM)

图是由结点和连接结点的边组成的集合。结点和边分别记作$v$和$e$，结点和边的集合分别记作$V$和$E$，图记作$G=(V，E)$，无向图是指边没有方向的图。
概率图模型是一类用图的形式表示随机变量之间条件依赖关系的概率模型，是概率论与图论的结合。根据图中边有无方向，常用的概率图模型分为两类：有向图（贝叶斯网络、信念网络）、无向图（马尔可夫随机场、马尔可夫网络）。
(1)有向图
有向图的联合概率如下：
$$
P(X_{1},X_{2},……,X_{n})=\prod_{i=1}^{N}P(X_{i}|\pi(X_{i}))
$$
其中$\pi(X_{i})$是$X_{i}$的父节点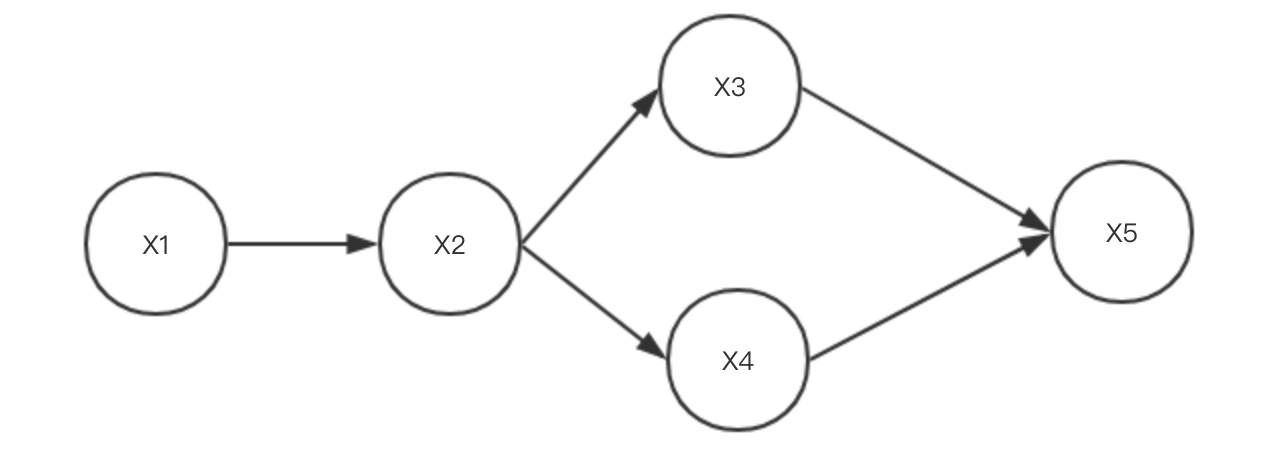

如上图所示则有：
$$
P(X_{1},X_{2},X_{3},….,X_{5})=P(X_{1})P(X_{2}|X_{1})P(X_{3}|X_{2})P(X_{4}|X_{2})P(X_{5}|X_{3},X_{4})
$$

(2)概率无向图模型
设有联合概率分布$P(Y)$，由无向图$G=(V,E)$表示，在图G中，结点表示随机变量，边表示随机变量之间的依赖关系。如果联合概率分布$P(Y)$满足成对、局部或全局马尔可夫性，就称此联合概率分布为概率无向图模型或马尔可夫随机场。
尽管在给定每个节点的条件下，分配给该节点一个条件概率是可能的，无向图的无向性导致我们不能用条件概率参数化表示联合概率，而要从一组条件独立的原则中找出一系列局部函数的乘积来表示联合概率。

2.2、马尔可夫性

2.2.1、成对马尔可夫性

成对马尔可夫性:设$u$和$v$是无向图$G$中任意两个没有边链接的节点，节点$u$和$v$分别对应随机变量$Y_{u}$和$Y_{v}$,其他所有节点为$O$对应的随机变量组是$Y_{O}$。成对马尔可夫性是指在给定随机变量组$Y_{O}$的条件下随机变量$Y_{u}$和$Y_{v}$是条件独立的，即：
$$
P(Y_{u},Y_{v}|Y_{O})=P(Y_{u}|Y_{O})P(Y_{v}|Y_{O})
$$

2.2.2、局部马尔可夫性

局部马尔可夫性：设$v\in V$是无向图$G$中任意一个结点，$W$是与$v$有边连接的所有结点，$O$是$v$、$W$以外的其他所有结点。$v$表示的随机变量是$Y_{v}$，$W$表示的随机变量组是$Y_{W}$，$O$表示的随机变量组是$Y_{O}$。如下图所示：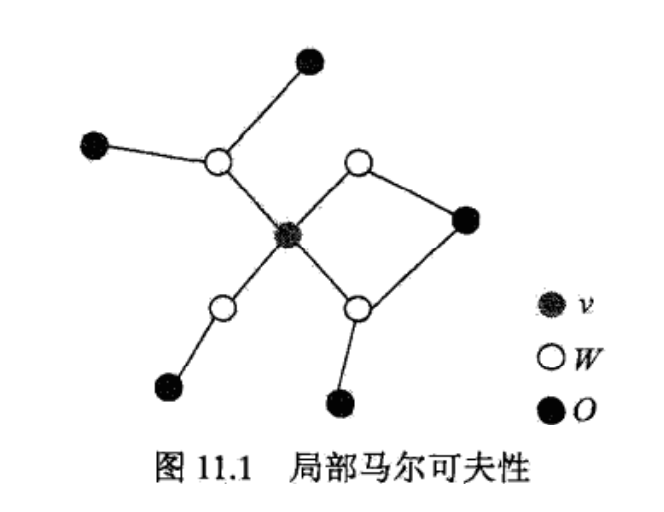

局部马尔可夫性是指在给定随机变量组$Y_{W}$的条件下随机变量$Y_{v}$与随机变量$Y_{O}$是独立的，即：
$$
P(Y_{v},Y_{O}|Y_{W})=P(Y_{v}|Y_{W})P(Y_{O}|Y_{W})
$$
设在$P(Y_{O}|Y_{W})>0$时等价的：
$$
P(Y_{v}|Y_{W})=P(Y_{v}|Y_{W},Y_{O})
$$

2.2.3、全局马尔可夫性

全局马尔可夫性：设结点集合A,B是在无向图G中被结点集合C分开的任意结点集合，如下图所示。结点结合A,B和C所对应的随机变量组分别是$Y_{A}$,$Y_{B}$和$Y_{C}$。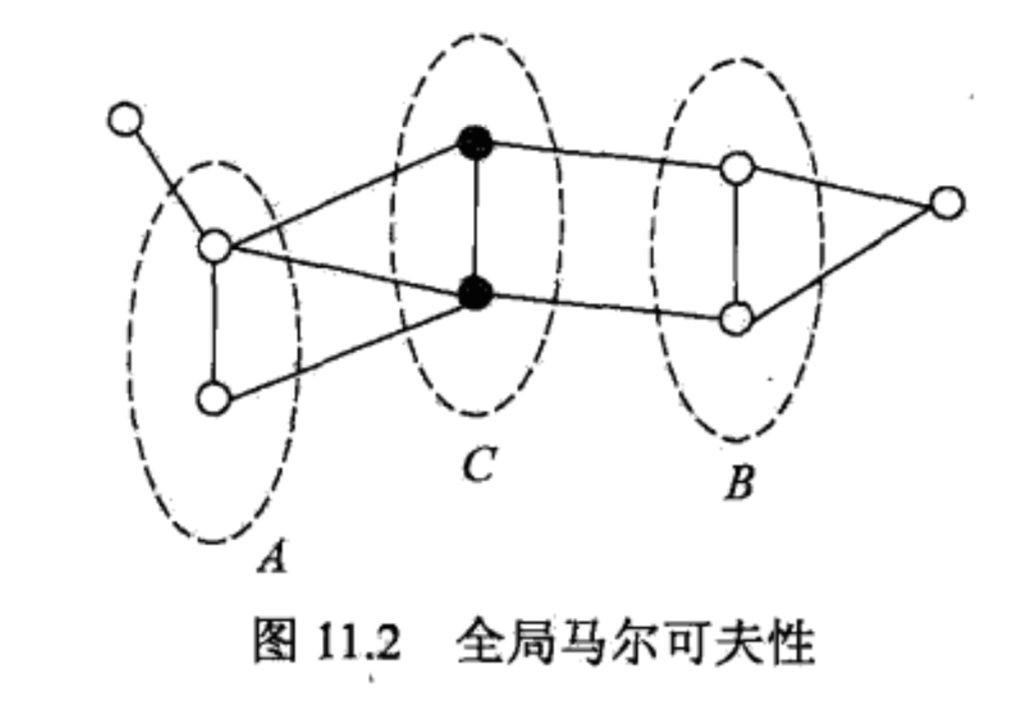

全局马尔可夫性是指给定随机变量组$Y_{C}$条件下随机变量组$Y_{A}$和$Y_{B}$是条件独立的，即
$$
P(Y_{A},Y_{B}|Y_{C})=P(Y_{A}|Y_{C})P(Y_{B}|Y_{C})
$$
上述成对、局部、全局马尔可夫性的定义是等价的。

2.3、团与最大团

无向图G中任何两个结点均有边连接的结点子集成为团(clique)。若C是无向图G中的一个团，并且不能在加进任何一个G的结点使其成为一个更大的团，则成为此C为最大团(maximal clique).
如下图所示的4个结点组成的无向图。途中由两个结点组成的团有5个：{$Y_{1},Y_{2}$},{$Y_{2},Y_{3}$},{$Y_{3},Y_{4}$},{$Y_{4},Y_{2}$}和{$Y_{1},Y_{3}$}.有两个最大团：{$Y_{1},Y_{2},Y_{3}$},{$Y_{2},Y_{3},Y_{4}$},而{$Y_{1},Y_{2},Y_{3},Y_{4}$}不是一个团，因为$Y_{1}$和$Y_{4}$没有边连接。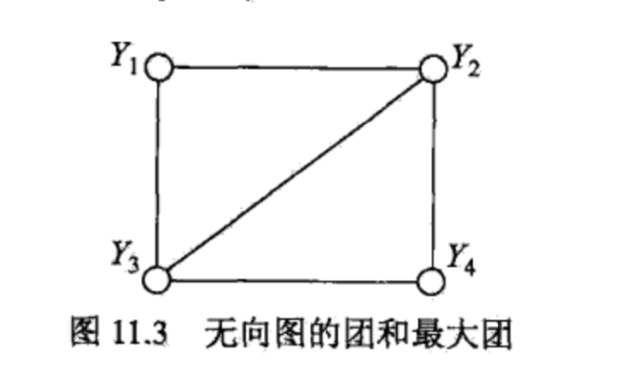
团与最大团
将概率无向图模型的联合概率分布表示为其最大团上的随机变量的函数的乘积形式的操作，成为概率无向图的模型因子分解。
给定概率无向图模型，设其无向图为G，C为G上的最大团，$Y_{C}$表示C对应的随机变量。那么概率无向图模型的联合概率P(Y)可写作所有最大团C上的函数$\Psi_{C}(Y_{C})$的乘积形式，即：
$$
P(Y)=\frac{1}{Z}\prod_{C}\Psi_{C}(Y_{C})
$$
其中，Z是规范化因子由下列式子给出：
$$
Z=\sum_{Y}\prod_{C}\Psi_{C}(Y_{C})
$$
规范化因子保证P(Y)构成一个概率分布。函数$\Psi_{C}(Y_{C})$称为势函数。这里要求势函数$\Psi_{C}(Y_{C})$是严格正的，通常定义为指函数:
$$
\Psi_{C}(Y_{C})=exp(-E(Y_{C}))
$$
概率无向图模型的因子分解由Hammersley-Cliford定理保证。

Hammersley-Cliford定理：
概率无向图模型的联合概率分布P(Y)可以表示为如下形式：
$$
P(Y)=\frac{1}{Z}\prod_{C}\Psi_{C}(Y_{C})
Z=\sum_{Y}\prod_{C}\Psi_{C}(Y_{C})
$$
其中，C是无向图的最大团，$Y_{C}$是C对应的结点对应的随机变量，$\Psi_{C}(Y_{C})$是C上定义的严格正函数，乘积是在无向图所有的最大团上进行的。

三、条件随机场

3.1、定义

设$G=(V,E)$是一个无向图，$Y={Y_{v}|v\in V}$是以G中节点为索引的随机变量$Y_{v}$构成的集合。在给定X的条件下，如果每个随机变量$Y_{v}$服从马尔可夫属性即$P(Y_{v}|X,Y_{u},u \neq v)=P(Y_{v}|X,Y_{u},u\sim v)$其中$u\sim v$表示u和v是相邻的边，则$(X,Y)$就构成一个随机条件场。

CRFs是在给定需要标定的观测序列的条件下，计算整个观测序列的联合概率，即求条件分布$P(S|O)$，而不是在给定当前的状态条件下，定义下一个状态的分布(HMM),即求联合分布P(S,O)。

3.2、线性CRFs模型(Linear-chain CRFs)

3.2.1、参数化形式

令$x={x_1,x_2,x_3,….,x_n}$为观测序列
$y={y_1,y_2,y_3,….,y_n}$为有限状态集合
根据随机场的基本理论：
$$
P(y|x,\lambda) \propto exp\Bigg(\sum_{i,j}\lambda_{j}t_{j}(y_{i-1},y_{i},x,i)+\sum_{i,k}\mu_{k}s_{k}(y_{i},x,i)\Bigg)
$$

$t_{j}(y_{i-1},y_{i},x,i)$:对于观测序列的标记位置i-1与i之间的特征转移函数
$s_{k}(y_{i},x,i)$:观测序列的i位置的状态特征函数
$\lambda_{j}$和$\mu_{k}$是权值
$Z(x)$是规范因子

通常$t_{j}$和$s_{k}$取值为0和1。当满足特征条件的时候取值为1，否则为0。条件随机场完全由特征函数$t_{j}$、$s_{k}$和对应的权值$\lambda_{j}$、$\mu_{k}$决定。

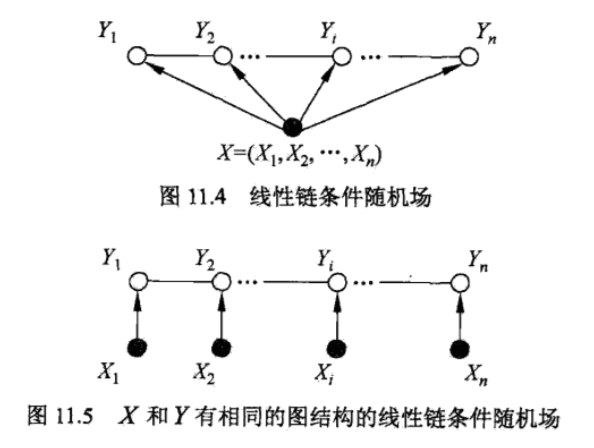
线性随机条件场
上式子表示在给定输入序列$x$，对应输出序列$y$预测的条件概率

例子：
列子01
列子02

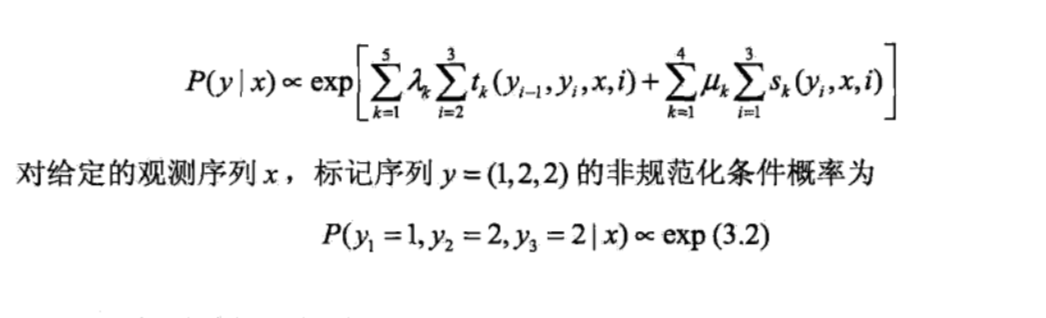
3.2.2、简化形式

为简便起见，首先将特征转移函数和状态特征函数及其对应的权值用统一的符号表示，设有$N_{1}$个转移特征，$N_{2}$个状态特征，$N=N_{1}+N_{2}$,记
$$
f_{n}(y_{i-1},y_{i},x,i)=\begin{cases}
t_{j}(y_{i-1},y_{i},x,i),n=1,2,…,N_{1}\\
s_{k}(y_{i},x,i), n=N_{1}+k,k=1,2,,….,N_{2}
\end{cases}
$$
然后，对特征转移和状态特征的各个位置的$i$求和，记作:
$$
f_{n}(y,x)=\sum_{i=1}^{N}f_{n}(y_{i-1},y_{i},x,i)
$$
用$w_{n}$表示特征$f_{n}(y,x)$的权值，即
$$
w_{n}=\begin{cases}
\lambda_{j},n=1,2,…,N_{1}\\
\mu_{k}, n=N_{1}+k,k=1,2,,….,N_{2}
\end{cases}
$$
于是随机条件场可以表示为:
$$
P(y|x)=\frac{1}{Z(x)}exp\sum_{n=1}^{N}w_{n}f_{n}(y,x) \\
Z(x)=\sum_{y}exp\sum_{n=1}^{N}w_{n}f_{n}(y,x)
$$
若以权值$w$表示权值向量，即
$$
w=(w_{1},w_{2},w_{3},….,w_{N})^T
$$
以$F(y,x)$表示全局特征向量，即：
$$
F(y,x)=(f_{1}(y,x),f_{2}(y,x),…..,f_{N}(y,x))^T
$$
则随机条件场可以写成向量$w$与$F(y,x)$的内积形式：
$$
P_{w}(y|x)=\frac{exp(w\cdot F(y,x))}{Z_{w}(x)}
$$
其中
$$
Z_{w}(x)=\sum_{y}exp(w\cdot F(y,x))
$$

四、条件随机场的概率计算问题

条件随机场的概率计算问题是指在给定条件随机场P(Y|X)，输入序列$x$和输出序列$y$，计算条件概率$P(Y_{t}=y_{i}|x)$,$P(Y_{i-1},Y_{i}=y_{i}|x)$以及相对应的数学期望问题。为了方便起见，像隐马尔可夫模型那样，引进前向-后向向量，递归地计算以上概率及期望值。这样的算法称为前向-后向算法

4.1、前向-后向算法

对每个指标$i=0,1,2….,n+1$，定义前向向量$\alpha_{i}(x)$：
$$
\alpha_{0}(y|x)=\begin{cases}
1,y=start \\
0,否则
\end{cases}
$$
递推公式为
$$
\alpha_{i}^{T}(y_{i}|x)=\alpha_{i-1}^{T}(y_{i-1}|x)M_{i}(y_{i-1},y_{i}|x),i=1,2,…,n+1
$$
又可以表示为：
$$
\alpha_{i}^{T}(x)=\alpha_{i-1}^{T}(x)M_{i}(x)
$$

$\alpha_{i}(x)$表示在位置i的标记是$y_{i}$并且到位置i的前部分标记序列的非规范化概率，$y_{i}$可取的值有m个，所以$\alpha_{i}(x)$是m维的列向量。
同样，对每个指标$i=0,1,2….,n+1$定义后向向量$\beta_{i}(x)$:
$$
\beta_{n+1}(y_{n+1}|x)=\begin{cases}
1,y_{n+1}=stop \\
0,否则
\end{cases} \\
\beta_{i}(y_{i}|x)=M_{i}(y_{i},y_{i+1}|x)\beta_{i-1}(y_{i+1}|x)
$$
又可以表示为
$$
\beta_{i}(x)=M_{i+1}(x)\beta_{i+1}(x)
$$
$\beta_{i}(y_{i}|x)$表示在位置i的标记为$y_{i}$,并且从i+1到n的后部分标记序列的非规范化概率。
由前向-后向向量定义不难得到：
$$
Z(x)=\alpha_{n}^{T}\cdot1=1^T\cdot\beta_{1}(x)
$$
这里$1$是元素均为1的m维列向量。

4.2、概率计算

按照前向-后向向量的定义，很容易计算标记序列在位置i是$y_{i}$的条件概率和在位置i-1与i是标记$y_{i-1}$和$y_{i}$的条件概率：
$$
P(Y_{i}=y_{i}|x)=\frac{\alpha_{i}^{T}(y_{i}|x)\beta_{i}(y_{i}|x)}{Z(x)} \\
P(Y_{i-1}=y_{i-1},Y_{i}=y_{i}|x)=\frac{\alpha_{i-1}^{T}(y_{i-1}|x)M_{i}(y_{i-1},y_{i}|x)\beta_{i}(y_{i}|x)}{Z(x)}
$$
其中
$$
Z(x)=\alpha_{n}^{T}\cdot1=1^T\cdot\beta_{1}(x)
$$

4.3、期望值的计算

利用前向-后向向量，可以计算特征函数关于联合分布$P(X,Y)$和条件分布$P(Y|X)$的数学期望。
特征函数$f_{k}$关于条件分布$F(Y|X)$的数学期望是
$$
\begin{multline}
E_{P(Y|X)}[f_{k}]=\sum_{k}P(y|x)f_{k}(y,x)\\
=\sum_{i=1}^{n+1}\sum_{y_{i-1},y_{i}}f_{k}(y_{i-1},y_{i},x,i)\frac{\alpha_{i-1}^{T}(y_{i-1}|x)M_{i}(y_{i-1},y_{i}|x)\beta_{i}(y_{i}|x)}{Z(x)},k=1,2,3,….,K
\end{multline}
$$

上文中的$f_{n}$变成$f_{k}$，且N=K

其中
$$
Z(x)=\alpha_{n}^{T}\cdot1=1^T\cdot\beta_{1}(x)
$$

假设经验分布$\hat{P}(x)$，特征函数$f_{k}$关于联合分布$F(X,Y)$的数学期望是
$$
\begin{split}
E_{P(X,Y)}[f_{k}]{} & =\sum_{x,y}P(X,Y)\sum_{i=1}^{n+1}f_{k}(y_{i-1},y_{i},x,i)\\
{} & =\sum_{x}\hat{P}(x)\sum_{y}P(y|x)\sum_{i=1}^{n+1}f_{k}(y_{i-1},y_{i},x,i)\\
{} & =\sum_{x}\hat{P}(x)\sum_{i=1}^{n+1}\sum_{y_{i-1},y_{i}}f_{k}(y_{i-1},y_{i},x,i)\frac{\alpha_{i-1}^{T}(y_{i-1}|x)M_{i}(y_{i-1},y_{i}|x)\beta_{i}(y_{i}|x)}{Z(x)},k=1,2,3,….,K
\end{split}
$$
其中
$$
Z(x)=\alpha_{n}^{T}\cdot1=1^T\cdot\beta_{1}(x)
$$
这个式子是特征函数数学期望的一般计算公式。对于转移特征$t_{k}(y_{i-1},y_{i},x,i)$,$k=1,2,3,…,K_{1}$,可以将式子中的$f_{k}$换成$t_{k}$;对于状态特征，可以将式中的$f_{k}$换成$s_{l}$,表示为$s_{l}(y_{i},x,i)$,k=K1+l,$l=1,2,3,…,K_{2}$。
有了这些式子，对于给定的观测序列x与标记序列y，可以通过一次前向扫描计算$\alpha_{i}$及$Z(x)$,通过一次后向扫描计算$\alpha_{i}$及$Z(x)$，通过一次后向扫描计算$\beta_{i}$。从而计算所有的概率和特征的期望

五、总结

简单理解，条件随机场是给定随机变量X条件下，随机变量Y的马尔可夫随机场,在条件概率模型中$P(Y|X)$中，Y是输出变量，表示标记序列，X是输入变量，表示观测序列。训练时候利用训练数据库，通过极大似然估计得到条件概率模型，然后使用该模型预测。
同时CRF是一个无向图的概率模型，顶点代表变量，顶点之间的边代表两个变量之间依赖关系。常用的是链式CRF结构，如此可以表达长距离依赖性，和交叠特征的能力。所有特征可以进行全局归一化，得到全局最优解。（因为同一特征在各个位置都有表示，可以将同一个特征在不同位置求和，将局部特征转化为全局特征，从而得到全局最优解。）
上面所述内容已经将条件随机场的基本知识点、模型以及概率计算问题解决了。学习和预测问题将在下一篇博文条件随机场之学习和预测问题中解决。

条件随机场之基本概念与模型