1、简介
隐马尔可夫(Hidden Markov model)模型是一类基于概率统计的模型,是一种结构最简单的动态贝叶斯网,是一种重要的有向图模型。自上世纪80年代发展起来,在时序数据建模,例如:语音识别、文字识别、自然语言处理等领域广泛应用。隐马尔可夫模型涉及的变量、参数众多,应用也很广泛。
2、隐马尔可夫模型的基本概念
2.1、隐马尔可夫模型的定义
隐马尔可夫模型是关于时序的概率模型,描述由一个隐藏的马尔可夫链随机生成不可观测的状态随机序列,再由各个状态生成一个观测而产生观测随机序列的过程。隐藏的马尔可夫链随机生成的状态的序列,称为状态序列(state sequence);每个状态生成一个观测,而由此产生的观测的随机序列,称为观测序列(observation sequence)。序列的每一个位置又可以看作是一个时刻。
什么叫隐马尔可夫链呢?就是每个状态的转移只依赖于之前的n个状态,这个过程被称为1个n阶的模型,其中n是影响转移状态的数目。最简单的马尔可夫过程就是一阶过程,每一个状态的转移只依赖于其之前的那一个状态。用数学表达式表示就是:
$$
P(X_{n+1}=x|X_{1}=x_{1},X_{2}=x_{2},X_{3}=x_{3},….X_{n}=x_{n})=P(X_{n+1}=x|X_{n}=x_{n})
$$
隐马尔可夫模型由初始概率分布、状态转移概率分布、以及观测概率分布确定,隐马尔可夫模型的定义如下:
设Q是所有可能的状态的集合,V是所有可能的观测的集合。
$$
Q={q_1,q_2,q_3,…..,q_N}, V={v_1,v_2,v_3,….,v_M}
$$
其中N是可能的状态数,M为可能的观测数。
状态q是不可见的,观测v是可见的。应用到词性标注系统,词就是v,词性就是q。
I是长度为T的状态序列,O是对应的观测序列。
$$
I=(i_1,i_2,…,i_T),O=(o_1,o_2,…,o_T)
$$
这可以想象为相当于给定了一个词(O)+词性(I)的训练集,于是我们手上有了一个可以用隐马尔可夫模型解决的实际问题。
定义A为状态转移概率矩阵:
$$
A=\Big[a_{ij}\Big]_{N \times N}
$$
其中,
$$
a_{tj}=P(i_{t+1}=q_j|i_{t}=q_i);i=1,2,…,N;j=1,2,…,N
$$
是在时刻t处于状态$q_i$的条件下在时刻t+1转移到状态$q_j$的概率。
这部分阐述的是马尔可夫的一阶过程,每一个状态的转移只依赖于其之前的那一个状态
B是观测概率矩阵:
$$
B=\Big[b_j(k)\Big]_{N \times M}
$$
其中,
$$
b_j(k)=P(o_t=v_k|i_{t}=q_j),k=1,2,….,M;j=1,2,…,N
$$
是在时刻t处于状态$q_j$的条件下生成观测$v_k$
这实际上在作另一个假设,观测是由当前时刻的状态决定的,跟其他因素无关.
$\pi$是初始状态概率向量:
$$
\pi=(\pi_{i})
$$
其中,
$$
\pi_{i}=P(i_1=q_i),i=1,2,…,N
$$
是时刻t=1处于状态$q_j$的概率。
隐马尔可夫模型由初始状态概率向量$\pi$、状态转移概率矩阵A和观测概率矩阵B决定。$\pi$和A决定状态序列,B决定观测序列。因此,隐马尔可夫模型$\lambda$可以用三元符号表示,即
$$
\lambda=(A,B,\pi)
$$
$(A,B,\pi)$称为隐马尔可夫模型的三要素。如果加上一个具体的状态集合Q和观测序列V,则构成了HMM的五元组。
状态转移概率矩阵A与初始状态概率向量$\pi$确定了隐藏的马尔可夫链,生成不可观测的状态序列。观测概率矩阵B确定了如何从状态生成观测,与状态序列综合确定了如何产生观测序列。
从定义可知,隐马尔可夫模型作了两个基本假设:
(1)齐次马尔可夫性假设,即假设隐藏的马尔可夫链在任意时刻t的状态只依赖于其前一时刻的状态,与其他时刻的状态及观测无关。
$$
p(i_t|i_{t-1},o_{t-1},….,i_1,o_1)=P(i_t|i_{t-1}),t=1,2,…,T
$$
(2)观测独立性假设,即假设任意时刻的观测只依赖于该时刻的马尔可夫链的状态,与其他观测及状态无关。
$$
P(o_t|i_T,o_T,i_{T-1},o_{T-1},….,i_{t+1},o_{t+1},i_t,i_{t-1},o_{t-1},…,i_1,o_1)=p(o_t|i_t)
$$
2.2、定义的实例说明
你本是一个城乡结合部修电脑做网站的小码农,突然春风吹来全民创业。于是跟村头诊所的老王响应总理号召合伙创业去了,有什么好的创业点子呢?对了,现在不是很流行什么“大数据”么,那就搞个“医疗大数据”吧,虽然只是个乡镇诊所……但管它呢,投资人就好这口。
数据从哪儿来呢?你把老王,哦不,是王老板的出诊记录都翻了一遍,发现从这些记录来看,村子里的人只有两种病情:要么健康,要么发烧。但村民不确定自己到底是哪种状态,只能回答你感觉正常、头晕或冷。有位村民是诊所的常客,他的病历卡上完整地记录了这三天的身体特征(正常、头晕或冷),他想利用王老板的“医疗大数据”得出这三天的诊断结果(健康或发烧)。
这时候王老板掐指一算,说其实感冒这种病,只跟病人前一天的病情有关,并且当天的病情决定当天的身体感觉。
于是你一拍大腿,天助我也,隐马尔可夫模型的两个基本假设都满足了,于是统计了一下病历卡上的数据,撸了这么一串Python代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15states = ('Healthy', 'Fever')
observations = ('normal', 'cold', 'dizzy')
start_probability = {'Healthy': 0.6, 'Fever': 0.4}
transition_probability = {
'Healthy': {'Healthy': 0.7, 'Fever': 0.3},
'Fever': {'Healthy': 0.4, 'Fever': 0.6}
}
emission_probability = {
'Healthy': {'normal': 0.5, 'cold': 0.4, 'dizzy': 0.1},
'Fever': {'normal': 0.1, 'cold': 0.3, 'dizzy': 0.6}
}
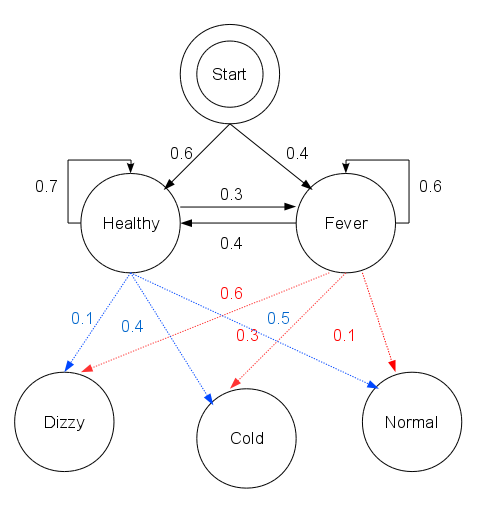
states代表病情,observations表示最近三天观察到的身体感受,start_probability代表病情的分布,transition_probability是病情到病情的转移概率,emission_probability则是病情表现出身体状况的发射概率。以上列出的就是隐马的五元组。
3、隐马尔可夫模型的3个基本问題
隐马尔可夫模型有3个基本问题:
- 概率计算问题。给定模型$(A,B,\pi)$观测序列$O=(o_1,o_2,….,o_T)$,计算在模型$\lambda$下观测序列O出现的概率$P(O|\lambda)$。
- 学习问题。己知观测序列$O=(o_1,o_2,….,o_T)$,估计模型$(A,B,\pi)$参数,使得在该模型下观测序列概率$P(O|\lambda)$最大。即用极大似然估计的方法估计参数。
- 预测问题,也称为解码(decoding)问题。已知模型$(A,B,\pi)$观测序列$O=(o_1,o_2,….,o_T)$求对给定观测序列条件概率$P(I|O)$最大的状态序列$I=(i_1,i_2,,,,,i_T)$。即给定观测序列,求最有可能的对应的状态序列。
下面各节将逐一介绍这些基本问题的解法。
3.1、概率计算算法
计算观测序列概率有前向(forward)与后向(backward)算法,以及概念上可行但计算上不可行的直接计算法(枚举)。前向后向算法无非就是求第一个状态的前向概率或最后一个状态的后向概率,然后向后或向前递推即可。
3.1.1、直接计算法
给定模型,求给定长度为T的观测序列的概率,直接计算法的思路是枚举所有的长度T的状态序列,计算该状态序列与观测序列的联合概率(隐状态发射到观测),对所有的枚举项求和即可。在状态种类为N的情况下,一共有$N^T$种排列组合,每种组合计算联合概率的计算量为T,总的复杂度为$O(TN^T)$,并不可取。
3.1.2、前向算法
定义(前向概率) 给定隐马尔可夫模型$\lambda$,定义到时刻t为止的观测序列为$o_1,o_2,…,o_t$且状态为$q_i$的概率为前向概率,记作
$$
\alpha_t(i)=P(o_1,o_2,…,o_t,i_t=q_i|\lambda)
$$
可以递推地求得前向概率$\alpha_t(i)$及观测序列概率$P(O|\lambda)$。
算法(观测序列概率的前向算法)
输入:隐马尔可夫模型$\lambda$,观测序列O;
输出:观测序列概率$P(O|\lambda)$
(1)初值
$$
\alpha_1(i)=\pi_{i}b_{i}(o_1),i=1,2,….,N
$$
前向概率的定义中一共限定了两个条件,一是到当前为止的观测序列,另一个是当前的状态。所以初值的计算也有两项(观测和状态),一项是初始状态概率,另一项是发射到当前观测的概率。
(2)递推对$t=1,2,….,T-1$
$$
\alpha_{t+1}(i)=\Big[\sum_{j=1}^{N}\alpha_t(j)a_{ji}\Big]b_i(o_{t+1})
$$
每次递推同样由两部分构成,大括号中是当前状态为i且观测序列的前t个符合要求的概率,括号外的是状态i发射观测t+1的概率。
(3)终止
$$
P(O|\lambda)=\sum_{i=1}^{N}\alpha_T(i)
$$
由于到了时间T,一共有N种状态发射了最后那个观测,所以最终的结果要将这些概率加起来。
由于每次递推都是在前一次的基础上进行的,所以降低了复杂度。准确来说,其计算过程如下图所示: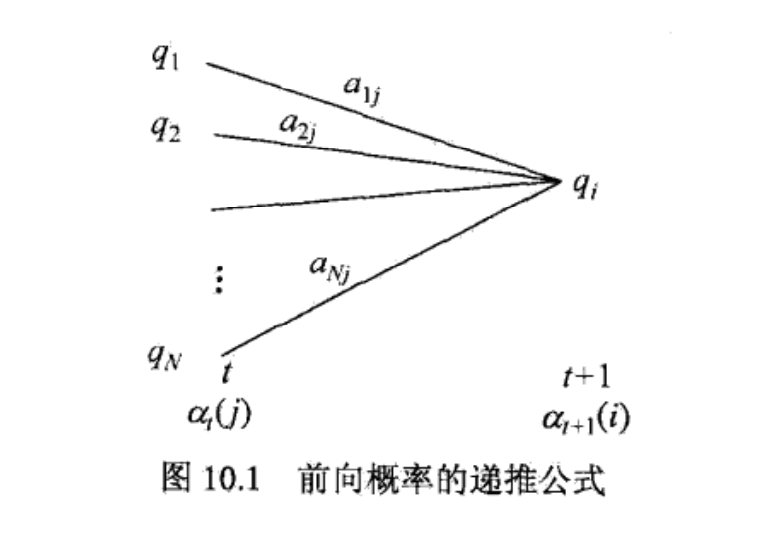
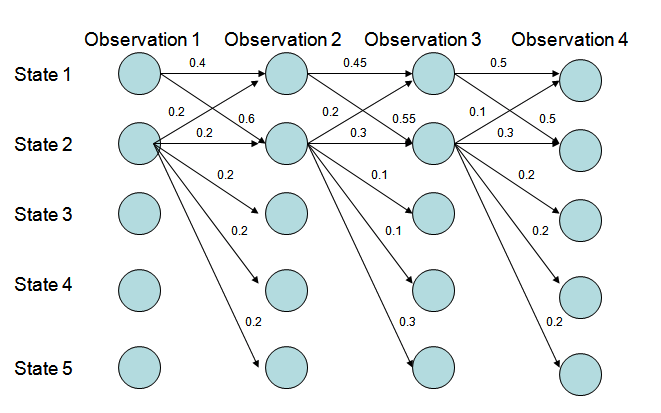
下方标号表示时间节点,每个时间点都有N种状态,所以相邻两个时间之间的递推消耗N^2次计算。而每次递推都是在前一次的基础上做的,所以只需累加O(T)次,所以总体复杂度是O(T)个$N^2$,即$O(N^{2}T)$。
前向算法Python实现1
2
3
4
5
6
7
8
9
10
11
12def _forward(self, obs_seq):
N = self.A.shape[0]
T = len(obs_seq)
F = np.zeros((N,T))
F[:,0] = self.pi * self.B[:, obs_seq[0]]
for t in range(1, T):
for n in range(N):
F[n,t] = np.dot(F[:,t-1], (self.A[:,n])) * self.B[n, obs_seq[t]]
return F
代码和伪码的对应关系还是很清晰的,F对应alpha,HMM的三个参数与伪码一致。
3.1.3、后向算法
定义(后向概率) 给定隐马尔可夫模型$\lambda$,定义在时刻t状态为$q_i$的条件下,从t+1到T的部分观测序列为$o_{t+1},o_{t+2},….,o_{T}$的概率为后向概率,记作
$$
\beta_{t}(i)=P(o_{t+1},o_{t+2},….,o_{T}|i_{T}=q_{i},\lambda)
$$
可以用递推的方法求得后向概率$\beta_t(i)$及观测序列概率$P(O|\lambda)$。
算法(观测序列概率的后向算法)
输入:隐马尔可夫模型$\lambda$,观测序列O;
输出:观测序列概率$P(O|\lambda)$
(1)初值
$$
\beta_T(i)=1,i=1,2,….,N
$$
根据定义,从T+1到T的部分观测序列其实不存在,所以硬性规定这个值是1。
(2)对$t=T-1,T-2,….,1$
$$
beta_t(i)=\sum_{j=1}^{N}a_{ij}b_j(a_{t+1})\beta_{t+1}(j),i=1,2,…,N
$$
$a_{ij}$表示状态i转移到j的概率,$b_j$表示发射$O_{t+1}$,$\beta_{t+1}(j)$表示j后面的序列对应的后向概率。
(3)
$$
P(O|\lambda)=\sum_{i=1}^{N}\pi_{i}b_i(o_1)\beta_1(i)
$$
最后的求和是因为,在第一个时间点上有N种后向概率都能输出从2到T的观测序列,所以乘上输出O1的概率后求和得到最终结果。
其计算过程如下图所示: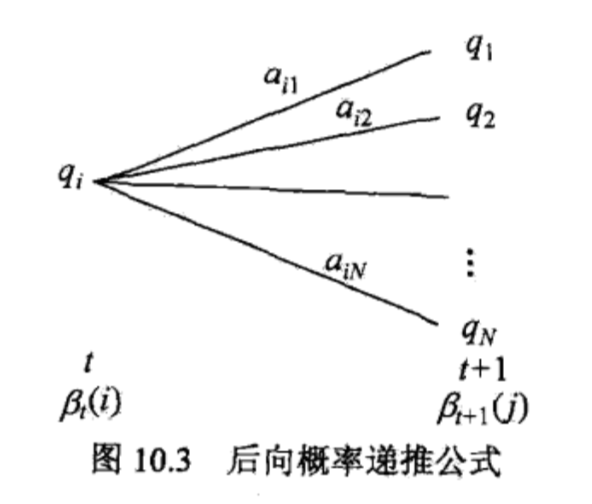
后向算法的Python实现1
2
3
4
5
6
7
8
9
10
11
12def _backward(self, obs_seq):
N = self.A.shape[0]
T = len(obs_seq)
X = np.zeros((N,T))
X[:,-1:] = 1
for t in reversed(range(T-1)):
for n in range(N):
X[n,t] = np.sum(X[:,t+1] * self.A[n,:] * self.B[:, obs_seq[t+1]])
return X
3.2、学习算法
隐马尔可夫模型的学习,根据训练数据是包括观测序列和对应的状态序列还是只有观测序列,可以分别由监督学习与非监督学习实现,下面主要介绍监督学习算法,而非监督学习算法–Baum-Weich算法(EM算法学习HMM参数的算法)因为无监督学习并不靠谱,而且也比较复杂,所以就不介绍了。
监督学习方法
转移概率$a_{ij}$的估计
设样本中时刻t处于状态i时刻t+1转移到状态j的频数为$A_{ij}$,那么状态转移概率$a_{ij}$的估计是
$$
\hat{a}_{ij}=\frac{A_{ij}}{\sum_{j=1}^{N}A_{ij}}
$$
很简单的最大似然估计。拿分词来举例吧,如果标注集合为B、M、E、S四个,那么假设$a_{ij}$是状态B转到E的概率,则有$A_{ij}$为在状态为B$\rightarrow$状态E的样本数,$\sum_{j=1}^{N}A_{ij}$则为在状态为B的情况下转移到B、M、E、S的样本数之和。此时为:
$$
\hat{a}_{B \rightarrow E}=\frac{count(B \rightarrow E)}{count(B \rightarrow B)+count(B \rightarrow M)+count(B \rightarrow E)+count(B \rightarrow S)}
$$观测概率的估计
设样本中状态为j并观测为k的频数是$B_{jk}$那么状态为j观测为k的概率的估计是
$$
\hat{b}_j(k)=\frac{B_{jk}}{\sum_{k=1}^{M}B_{jk}},j=1,2,…,N;k=1,2,…,M
$$同样拿分词来说,假定给定训练语料“我/S 来/B 到/E 北/B 京/E 大/B 学/M 城/E”,则有如下:
状态集合:B、M、E、S
观测集合(字的集合):我、来、到、北、京、大、学、城
假定$b_j(k)$为状态B $\rightarrow$ 观测“北”的概率,状态B的情况下的观测值有:来、北、大;则有:
$$
\hat{b}_B(北)=\frac{count(B \rightarrow 北)}{count(B \rightarrow 来)+count(B \rightarrow 北)+count(B \rightarrow 大)}
$$初始状态概率$\pi_i$的估计$\hat{\pi_i}$为S个样本中初始状态为$q_i$的频率。
同样还是拿分词来举例,假定给以如下的训练语料:
我/S 来/B 到/E 北/B 京/E 大/B 学/M 城/E
吉/B 林/M 省/E 长/B 春/M 市/E 长/B 春/E 药B/ 店/E
则初始状态的分布为{B:0.5,M:0,E:0,S:0.5},其实就是计算每个句子的开头第一个字的状态的概率。
由于监督学习需要使用训练数据,而人工标注训练数据往往代价很高,有时就会利用非监督学习的方法。
3.3、预测算法
维特比算法实际是用动态规划解隐马尔可夫模型预测问题,即用动态规划(dynamic programming)求概率最大路径(最优路径)。
算法(维特比算法)
输入:模型$\lambda=(A,B,\pi)$和观测序列$O=(o_1,o_2,…,o_T)$
输出:最优路径,即最优状态序列:$I^{*}=(i_{1}^{*},i_{2}^{*},…,i_{T}^{*})$
(1)初始化
$$
\begin{split}
{} & \delta_{1}(i)=\pi_{i}b_{i}(o_{1}),i=1,2,3,…,N \\
{} & \psi_{1}(i)=0,i=1,2,3,…,N
\end{split}
$$
(2)递推。对$t=2,3,…,T$
$$
\begin{split}
{} & \delta_{t}(i)=\max_{1 \leq j \leq N}[\delta_{t-1}(j)a_{ji}]b_{i}(o_{t}),i=1,2,…,N \\
{} & \psi_{t}(i)=arg \max_{1 \leq j \leq N}[\delta_{t-1}(j)a_{ji}],i=1,2,…,N
\end{split}
$$
$\delta_{t}(i)$:
(3)终止
$$
\begin{split}
{} & P^{*}=\max_{1 \leq i \leq N}\delta_{T}(i)
{} & i_{T}^{*}=arg \max_{1 \leq i \leq N}[\delta_{T}(i)]
\end{split}
$$
(4)最优路径回溯。对$t=T-1,T-2,…,1$
$$
i_{t}^{*}=\psi_{t+1}(i_{t+1}^{*})
$$
求得最优路径$I^{*}=(i_{1}^{*},i_{2}^{*},…,i_{T}^{*})$
维特比算法Python实现
不管是监督学习,还是非监督学习,我们反正都训练出了一个HMM模型。现在诊所来了一位病人,他最近三天的病状是:1
observations = ('normal', 'cold', 'dizzy')
如何用Viterbi算法计算他的病情以及相应的概率呢?1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26def viterbi(self, obs_seq):
"""
Returns
-------
V : numpy.ndarray
V [s][t] = Maximum probability of an observation sequence ending
at time 't' with final state 's'
prev : numpy.ndarray
Contains a pointer to the previous state at t-1 that maximizes
V[state][t]
"""
N = self.A.shape[0]
T = len(obs_seq)
prev = np.zeros((T - 1, N), dtype=int)
# DP matrix containing max likelihood of state at a given time
V = np.zeros((N, T))
V[:,0] = self.pi * self.B[:,obs_seq[0]]
for t in range(1, T):
for n in range(N):
seq_probs = V[:,t-1] * self.A[:,n] * self.B[n, obs_seq[t]]
prev[t-1,n] = np.argmax(seq_probs)
V[n,t] = np.max(seq_probs)
return V, prev
这应该是目前最简洁最优雅的实现了,调用方法如下:1
2
3
4
5
6
7
8
9
10h = hmm.HMM(A, B, pi)
V, p = h.viterbi(observations_index)
print " " * 7, " ".join(("%10s" % observations_index_label[i]) for i in observations_index)
for s in range(0, 2):
print "%7s: " % states_index_label[s] + " ".join("%10s" % ("%f" % v) for v in V[s])
print '\nThe most possible states and probability are:'
p, ss = h.state_path(observations_index)
for s in ss:
print states_index_label[s],
print p
输出结果如下:1
2
3
4
5
6normal cold dizzy
Healthy: 0.300000 0.084000 0.005880
Fever: 0.040000 0.027000 0.015120
The most possible states and probability are
Healthy Healthy Fever 0.01512
对算法有疑问的可以参考这段动画,将代码单步一遍,什么都明白了:
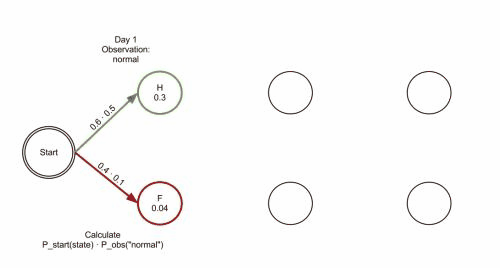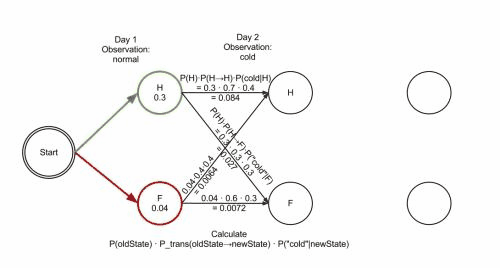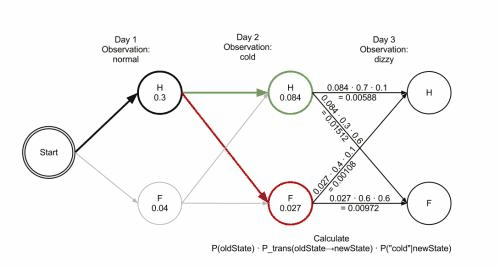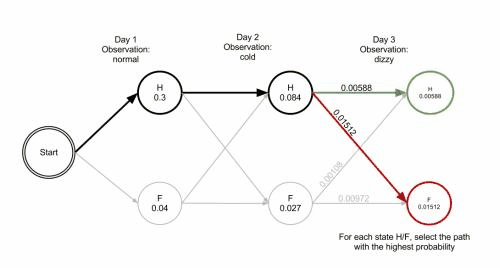
4、jieba分词的马尔可夫模型
jieba分词想必大家都知道,其分词模型分词部分就是使用了HMM完成的。在源码中有三个文件prob_trans.py为状态转移矩阵,prob_start.py为初始状态矩阵,prob_emit.py为发射矩阵。这三个文件都是训练好的模型文件。然后其使用维特比算法进行分词,我将其代码copy并进行适当修改打印出中间结果,代码如下:
1 | #!/usr/bin/python |
运行后结果如下: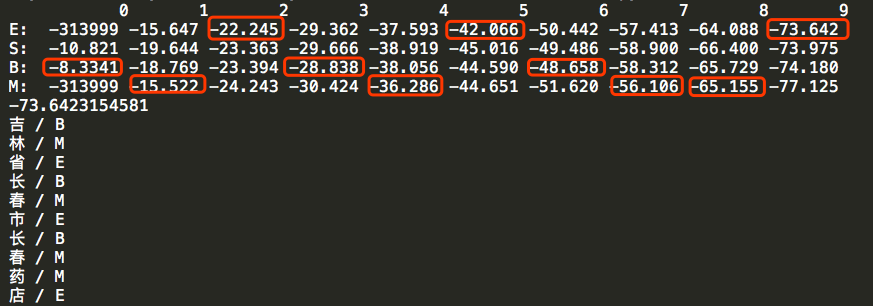
上面标红的结果练成一串就是最优路径,但是上面的结果很容易给大家造成误导,误导就是以为是求每一步的最优解就是结果,其实只是一种巧合和,局部最优并不一定是全局最优。其实在维特比求解的过程中,参照动态规划的最短路径的思想回溯,求得全局最优解。
5、参考
《统计学习方法》
Viterbi algorithm(wiki)
隐马尔可夫模型(码农场)
jieba分词的源码