一、EM算法简介
EM算法,指的是最大期望算法(Expectation Maximization Algorithm)是一种迭代算法,在统计学中被用于寻找,依赖于不可观察的隐性变量的概率模型中,参数的最大似然估计。最大期望算法经过两个步骤交替进行计算:计算期望(E),利用概率模型参数的现有估计值,计算隐藏变量的期望;最大化(M),利用E步上求得的隐藏变量的期望,对参数模型进行最大似然估计;M步上找到的参数估计值被用于下一个E步计算中,这个过程不断交替进行。所以称为EM算法(Expectation Maximization Algorithm)。
二、预备知识
在了解EM算法前我们先需要理解两个知识点:极大似然估计和Jensen不等式。
2.1、极大似然估计
极大似然估计方法(Maximum Likelihood Estimate,MLE)也称为最大概似估计或最大似然估计,是求估计的另一种方法,最大概似是1821年首先由德国数学家高斯(C. F. Gauss)提出。
最大似然估计的目的就是:利用已知的样本结果,反推最有可能(最大概率)导致这样结果的参数值。极大似然估计是建立在极大似然原理的基础上的一个统计方法,是概率论在统计学中的应用。极大似然估计提供了一种给定观察数据来评估模型参数的方法,即:“模型已定,参数未知”。通过若干次试验,观察其结果,利用试验结果得到某个参数值能够使样本出现的概率为最大,则称为极大似然估计。
(1) 举例说明:经典问题——学生身高问题
我们需要调查我们学校的男生和女生的身高分布。 假设你在校园里随便找了100个男生和100个女生。他们共200个人。将他们按照性别划分为两组,然后先统计抽样得到的100个男生的身高。假设他们的身高是服从正态分布的。但是这个分布的均值$\mu$和方差$\sigma^2$我们不知道,这两个参数就是我们要估计的。记作$\theta=[\mu,\sigma]^T$。
问题:我们知道样本所服从的概率分布的模型和一些样本,需要求解该模型的参数,如下图所示: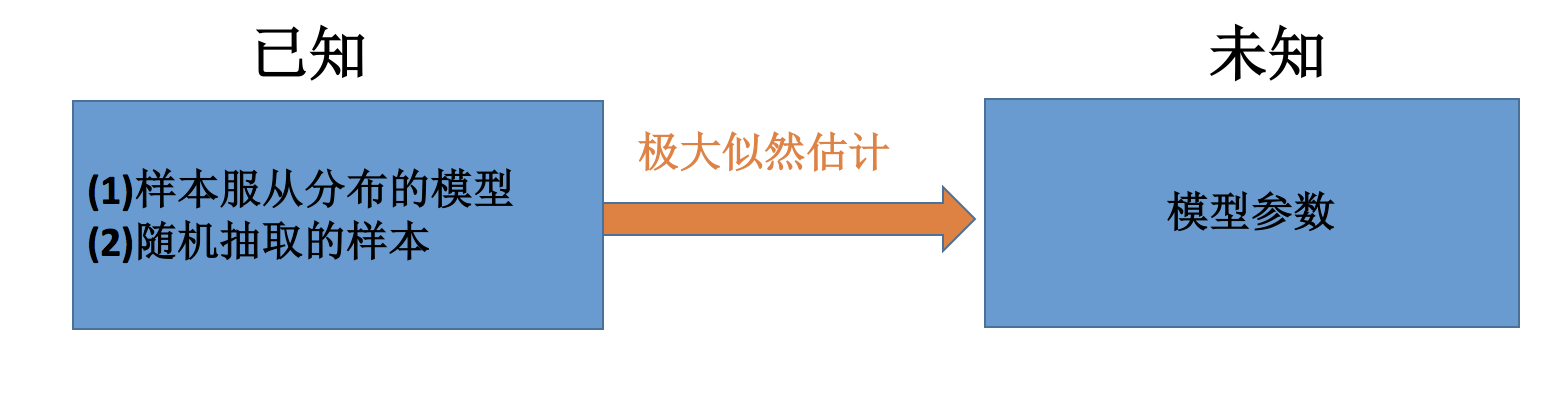
- 已知的:样本服从的分布模型、随机抽取的样本
- 未知的:模型的参数
根据已知条件,通过极大似然估计,求出未知参数。总的来说:极大似然估计就是用来估计模型参数的统计学方法。
(2) 如何估计
问题数学化:设样本集$X=x_1,x_2,…,x_N$,其中N=100 ,$p(x_i;\theta)$为概率密度函数,表示抽到男生$x_i$的身高的概率。由于100个样本之间独立同分布,所以我同时抽到这100个男生的概率就是他们各自概率的乘积,也就是样本集X中各个样本的联合概率,用下式表示:
$$
L(\theta)=L(x_1,x_2,….,x_n;\theta)=\prod_{i=1}^{n}p(x_i;\theta),\theta \in \Theta
$$
这个概率反映了,在概率密度函数的参数是$\theta$时,得到X这组样本的概率。 我们需要找到一个参数$\theta$,使得抽到X这组样本的概率最大,也就是说需要其对应的似然函数$L(\theta)$最大。满足条件的$\theta$叫做$\theta$的最大似然估计量,记为:
$$
\hat{\theta}=argmaxL(\theta)
$$
(3) 求最大似然函数估计值的一般步骤
首先,写出似然函数:
$$
L(\theta)=L(x_1,x_2,….,x_n;\theta)=\prod_{i=1}^{n}p(x_i;\theta),\theta \in \Theta
$$
然后,对似然函数取对数:
$$
H(\theta)=logL(\theta)=log\prod_{i=1}^{n}p(x_i;\theta)=\sum_{i=1}^{n}logp(x_i;\theta)
$$
在此我们取了一个对数似然,有两点优势,一个就是可以将乘法转换为加法,第二个取对数是单调上升函数,取最大似然和取对数最大似然目标是一致的
(4)求最大似然函数估计值的一般步骤
- 写出似然函数;
- 对似然函数取对数,并整理;
- 求导数,令导数为0,得到似然方程;
- 解似然方程,得到的参数即为所求;
2.2、Jensen不等式
Jensen不等式的意义是:如果对于所有的实数x,f(x)为凸函数(即f(x)的二阶导大于等于0),则函数的期望大于等于期望的函数(当且仅当x为常量时取等号),即
$$
E(f(x))\ge f(E(x))
$$
或者写成凸函数条件表达式的形式,在这个表达式式中,t相当于$x_1$的概率,(1−t)相当于$x_2$的概率:
$$
tf(x_1)+(1−t)f(x_2)\ge f(tx_1+(1−t)x_2); t\in{0,1}
$$
Jensen不等式应用于凹函数时,不等号方向反向。当且仅当X是常量时,Jensen不等式等号成立。
三、EM算法详解
还是回到上文中身高问题,假设男生、女生的身高分别服从各自的正态分布,则每个样本是从哪个分布抽取的,我们目前是不知道的。这个时候,对于每一个样本,就有两个方面需要猜测或者估计: 这个身高数据是来自于男生还是来自于女生?男生、女生身高的正态分布的参数分别是多少?EM算法要解决的问题正是这两个问题。
3.1、EM算法推导
给定的训练样本是$X={x_1,…,x_m}$,样例间独立,我们想找到每个样例隐含的类别$z$,能使得$p(x,z)$最大。$p(x,z)$的最大似然估计如下:
$$
H(\theta)=\sum_{i=1}^{m}logp(x_i;\theta)=\sum_{i=1}^{m}log\sum_{z_i}p(x_i,z_i;\theta)
$$
第一步是对极大似然取对数,第二步是对每个样例的每个可能类别z求联合分布概率和。但是直接求$\theta$一般比较困难,因为有隐藏变量$z$存在,但是一般确定了$z$后,求解就容易了。
EM是一种解决存在隐含变量优化问题的有效方法。既然不能直接最大化$H(\theta)$,我们可以不断地建立$H(\theta)$的下界(E步),然后优化下界(M步)。
对于每一个样例$i$,让$Q_i$表示该样例隐含变量$z$的某种分布,$Q_i$满足的条件是$\sum_{z}Q_i(z)=1,Q_i(z)\ge 0$。(如果$z$是连续性的,那么$Q_i$是概率密度函数,需要将求和符号换做积分符号)。比如要将班上学生聚类,假设隐藏变量$z$是身高,那么就是连续的高斯分布。如果按照隐藏变量是男女,那么就是伯努利分布了。
可以由前面阐述的内容得到下面的公式:
$$
\begin{split}
\sum_{i}logp(x_i;\theta) {} & =\sum_{i}log\sum_{z_i}p(x_i,z_i)\quad\quad\quad\quad(1)\\
{} & =\sum_{i}log\sum_{z_i}Q_i(z_i)\frac{p(x_i,z_i;\theta)}{Q_i(z_i)}\quad(2)\\
{} & \ge\sum_{i}\sum_{z_i}Q_i(z_i)log\frac{p(x_i,z_i;\theta)}{Q_i(z_i)}\quad(3)
\end{split}
$$
(1)到(2)比较直接,就是分子分母同乘以一个相等的函数。(2)到(3)利用了Jensen不等式,考虑到$log(x)$是凹函数(二阶导数小于0),而且$\sum_{z_i}Q_i(z_i)\frac{p(x_i,z_i;\theta)}{Q_i(z_i)}$就是$[p(x_i,z_i;\theta)/Q_i(z_i)]$的期望。详细了解参考博客the EM algorithm
上述过程可以看作是对$logL(\theta)$即$L(\theta)$)求了下界。对于$Q_i(z_i)$的选择,有多种可能,那么哪种更好呢?假设$\theta$已经给定,那么$logL(\theta)$的值就取决于$Q_i(z_i)$和$p(x_i,z_i)$了。我们可以通过调整这两个概率使下界不断上升,以逼近$logL(\theta)$的真实值,那么什么时候算是调整好了呢?当不等式变成等式时,说明我们调整后的概率能够等价于$logL(\theta)$了。按照这个思路,我们要找到等式成立的条件。根据Jensen不等式,要想让等式成立,需要让随机变量变成常数值,这里得到:
$$
\frac{p(x_i,z_i;\theta)}{Q_i(z_i)}=c
$$
c为常数,不依赖于$z_i$。对此式做进一步推导:由于$\sum_{z_i}Q_i(z_i)=1$,则有$\sum_{z_i}p(x_i,z_i;θ)=c$(多个等式分子分母相加不变,则认为每个样例的两个概率比值都是$c$),因此得到下式:
$$
Q(z_i)=\frac{p(x_i,z_i;\theta)}{\sum_{z_i}p(x_i,z_i;\theta)}=\frac{p(x_i,z_i;\theta)}{p(x_i;\theta)}=p(z_i|x_i;\theta)
$$
至此,我们推出了在固定其他参数$\theta$后,$Q_i(z_i)$的计算公式就是后验概率,解决了$Q_i(z_i)$如何选择的问题。这一步就是E步,建立$logL(\theta)$的下界。接下来的M步,就是在给定$Q_i(z_i)$后,调整$\theta$,去极大化$logL(\theta)$的下界(在固定$Q_i(z_i)$后,下界还可以调整的更大)。
3.2、EM算法流程
(1)初始化分布参数θ;
(2) 重复以下E、M步骤直到收敛
- E步骤:根据参数θ初始值或上一次迭代所得参数值来计算出隐性变量的后验概率(即隐性变量的期望),作为隐性变量的现估计值:
$$
Q_i(z_i):=p(z_i|x_i;\theta)
$$ - M步骤:将似然函数最大化以获得新的参数值:
$$
\theta:=arg\max_{\theta}\sum_{i}\sum_{z_i}Q_i(z_i)log\frac{p(x_i,z_i;\theta)}{Q_i(z_i)}
$$
3.3、EM算法优缺点
- 优点:算法简单,稳定上升的步骤能非常可靠地找到“最优的收敛值。
- 缺点:当所要优化的函数不是凸函数时,EM算法容易给出局部最佳解,而不是最优解;对初始值敏感:EM算法需要初始化参数θ,而参数θ的选择直接影响收敛效率以及能否得到全局最优解。
- EM算法的应用:k-means算法是EM算法思想的体现,E步骤为聚类过程,M步骤为更新类簇中心。GMM(高斯混合模型)也是EM算法的一个应用。
四、参考
- (EM算法)The EM Algorithm
- 机器学习系列之EM算法
- 《统计机器学习方法》,李航
- 《机器学习》,周志华