1、SVD定义

SVD(singular value decomposition)，翻译成中文就是奇异值分解。SVD的用处有很多，比如：LSA（隐性语义分析）、推荐系统、特征压缩（或称数据降维）。SVD可以理解为： 将一个比较复杂的矩阵用更小更简单的3个子矩阵的相乘来表示，这3个小矩阵描述了大矩阵重要的特性 。

2、SVD的原理

2.1、普通方阵的矩阵分解（EVD）

我们知道如果一个矩阵 A 是方阵，即行列维度相同（mxm），一般来说可以对 A 进行特征分解：
$$
A = U \Lambda U^{-1}
$$
其中，U 的列向量是 A 的特征向量，Λ 是对角矩阵，Λ 对角元素是对应特征向量的特征值。

举个简单的例子，例如方阵 A 为：
$$
\begin{equation}
A=\left[
\begin{matrix}
1&2\\
2&2
\end{matrix}
\right]
\end{equation}
$$

那么对其进行特征分解，相应的 Python 代码为：

import numpy as np

A = np.array([[2,2],[1,2]])
lamda,U=np.linalg.eig(A)
print('方阵 A: ',A)
print('特征值 lamda: ',lamda)
print('特征向量 U: ',U)

结果为:

方阵 A: [[2 2]
[1 2]]
特征值 lamda: [ 3.41421356 0.58578644]
特征向量 U: [[ 0.81649658 -0.81649658]
[ 0.57735027 0.57735027]]

$$
\begin{equation}
A=\left[
\begin{matrix}
1&2\\
2&2
\end{matrix}
\right] = \\
\left[
\begin{matrix}
0.81649658&-0.81649658\\
0.57735027&0.57735027
\end{matrix}
\right]
\left[
\begin{matrix}
3.41421356&0\\
0&0.58578644
\end{matrix}
\right]
\left[
\begin{matrix}
0.81649658&-0.81649658\\
0.57735027&0.57735027
\end{matrix}
\right]^{-1}
\end{equation}
$$

$$
A = U \Lambda U^{-1}
$$

其中，特征值$\lambda_{1}=3.41421356$，对应的特征向量$u_1$=[0.81649658 0.57735027]；特征值$\lambda_{2}=0.58578644$，对应的特征向量 $u_2$=[-0.81649658 0.57735027]，特征向量均为列向量。

值得注意的是，特征向量都是单位矩阵，相互之间是线性无关的，但是并不正交。得出的结论是对于任意方阵，不同特征值对应的特征向量必然线性无关，但是不一定正交。

2.2、对称矩阵的矩阵分解（EVD）

如果方阵 A 是对称矩阵，例如：
$$
\begin{equation}
A=\left[
\begin{matrix}
2&1\\
1&1
\end{matrix}
\right]
\end{equation}
$$
对称矩阵特征分解满足以下公式：
$$
A = U \Lambda U^{T}
$$
分解后结果如下：

方阵 A: [[2 1]
[1 1]]
特征值 lamda: [ 2.61803399 0.38196601]
特征向量 U: [[ 0.85065081 -0.52573111]
[ 0.52573111 0.85065081]]

其中，特征值$\lambda_{1}$=2.61803399，对应的特征向量$u_1$=[0.85065081 0.52573111]；特征值$\lambda_{2}$=0.38196601，对应的特征向量 $u_2$=[-0.52573111 0.85065081]，特征向量均为列向量。

注意，我们发现对阵矩阵的分解和非对称矩阵的分解除了公式不同之外，特征向量也有不同的特性。对称矩阵的不同特征值对应的特征向量不仅线性无关，而且是相互正交的。什么是正交呢？就是特征向量内积为零。验证如下：

$$0.85065081 * -0.52573111 + 0.52573111 * 0.85065081 \\
= 00.85065081 * −0.52573111+0.52573111 * 0.85065081=0$$

重点来了，对称矩阵 A 经过矩阵分解之后，可以写成以下形式：
$$
A=\lambda_{1}u_{1}u_{1}^{T}+\lambda_{2}u_{2}u_{2}^{T}
$$
对上式进行验证：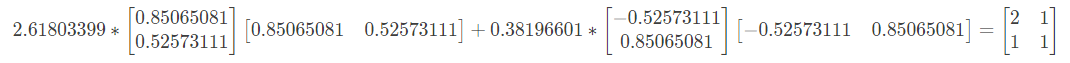

2.3、奇异值分解（SVD）

我们发现，在矩阵分解里的A是方阵或者是对称矩阵，行列维度都是相同的。但是实际应用中，很多矩阵都是非方阵、非对称的。那么如何对这类矩阵进行分解呢？因此，我们就引入了针对维度为 mxn 矩阵的分解方法，称之为奇异值分解（Singular Value Decomposition）
假设矩阵A的维度为mxn，虽然A不是方阵，但是下面的矩阵却是方阵，且维度分别为 mxm、nxn。
$$
AA^T 和 A^{T}A
$$
因此，我们就可以分别对上面的方阵进行分解：
$$
AA^{T}=P \Lambda_{1} P^{T} \\
A^{T}A=Q \Lambda_{2} Q^{T}
$$
其中,$\Lambda_{1}$和$\Lambda_{2}$是对焦矩阵，且对角线上非零元素均相同，即两个方阵具有相同的非零特征值，特征值令为$\sigma_1, \sigma_2, … , \sigma_k$。值得注意的是，k<=m 且 k<=n。

根据$\sigma_1, \sigma_2, … , \sigma_k$就可以得到矩阵A的特征值为:
$$
\lambda_{1}=\sqrt{\sigma_1},\lambda_{2}=\sqrt{\sigma_2},\lambda_{3}=\sqrt{\sigma_3},……,\lambda_{k}=\sqrt{\sigma_k}
$$
接下来，我们就能够得到奇异值分解的公式：
$$
A=P \Lambda Q^{T}
$$
其中，P 称为左奇异矩阵，维度是 mxm，Q称为右奇异矩阵，维度是 nxn。$\Lambda$并不是方阵，其维度为 mxn，$\Lambda$对角线上的非零元素就是A的特征值$\lambda_{1},\lambda_{2},…,\lambda_{k}$。图形化表示奇异值分解如下图所示：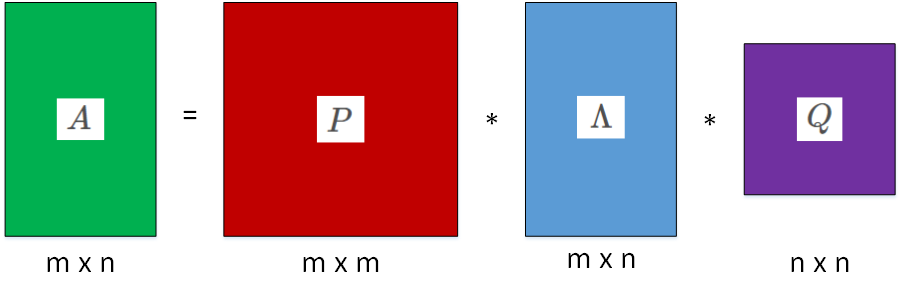
分解示意图

2.4、SVD的一些性质

对于奇异值,它跟我们特征分解中的特征值类似，在奇异值矩阵中也是按照从大到小排列，而且奇异值的减少特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。也就是说，我们也可以用最大的k个的奇异值和对应的左右奇异向量来近似描述矩阵。也就是说：
$$
A_{m \times n} = P_{m \times m} \Lambda_{m \times n} Q_{n \times n}^{T} \approx P_{m \times k} \Lambda_{k \times k} Q_{k \times n}^{T}
$$

其中k要比n小很多，也就是一个大的矩阵A可以用三个小的矩阵$P_{m \times k},\Lambda_{k \times k},Q_{k \times n}^{T}$来表示。如下图所示，现在我们的矩阵A只需要灰色的部分的三个小矩阵就可以近似描述了。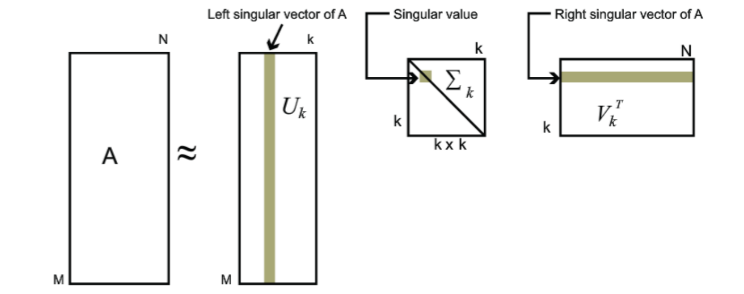
降维示意图

由于这个重要的性质，SVD可以用于PCA降维，来做数据压缩和去噪。也可以用于推荐算法，将用户和喜好对应的矩阵做特征分解，进而得到隐含的用户需求来做推荐。同时也可以用于NLP中的算法，比如潜在语义索引（LSI）。

3、SVD的应用

3.1、SVD在PCA中的应用

在PCA降维的过程中，需要找到样本协方差矩阵$X^{T}X$的最大的d个特征向量，然后用这最大的d个特征向量张成的矩阵来做低维投影降维。可以看出，在这个过程中需要先求出协方差矩阵$X^{T}X$，当样本数多样本特征数也多的时候，这个计算量是很大的。

注意到我们的SVD也可以得到协方差矩阵$X^{T}X$最大的d个特征向量张成的矩阵，但是SVD有个好处，有一些SVD的实现算法可以不求先求出协方差矩阵$X^{T}X$，也能求出我们的右奇异矩阵Q。也就是说，我们的PCA算法可以不用做特征分解，而是做SVD来完成。这个方法在样本量很大的时候很有效。实际上，scikit-learn的PCA算法的背后真正的实现就是用的SVD，而不是我们我们认为的暴力特征分解。

另一方面，注意到PCA仅仅使用了我们SVD的右奇异矩阵，没有使用左奇异矩阵，那么左奇异矩阵有什么用呢？

假设我们的样本是m×n的矩阵X，如果我们通过SVD找到了矩阵$XX^{T}$最大的d个特征向量张成的m×d维矩阵P，则我们如果进行如下处理：
$$
X_{d \times n}^{’}=P_{d \times m}^{T}X_{m \times n}
$$

可以得到一个d×n的矩阵$X^{’}$,这个矩阵和我们原来的m×n维样本矩阵X相比，行数从m减到了d，可见对行数进行了压缩。也就是说，左奇异矩阵可以用于行数的压缩。相对的，右奇异矩阵可以用于列数即特征维度的压缩，也就是我们的PCA降维。

3.2、SVD在主题模型中的应用(LSI/LSA)

潜在语义索引(LSI)，又称为潜在语义分析(LSA)，主要是在解决两类问题，一类是一词多义，如“bank”一词，可以指银行，也可以指河岸；另一类是一义多词，即同义词问题，如“car”和“automobile”具有相同的含义，如果在检索的过程中，在计算这两类问题的相似性时，依靠余弦相似性的方法将不能很好的处理这样的问题。所以提出了潜在语义索引的方法，利用SVD降维的方法将词项和文本映射到一个新的空间。

LSI是最早出现的主题模型了，它的算法原理很简单，一次奇异值分解就可以得到主题模型，同时解决词义的问题，非常漂亮。但是LSI有很多不足，导致它在当前实际的主题模型中已基本不再使用。主要的问题有：

SVD计算非常的耗时，尤其是我们的文本处理，词和文本数都是非常大的，对于这样的高维度矩阵做奇异值分解是非常难的。
主题值的选取对结果的影响非常大，很难选择合适的k值。
LSI得到的不是一个概率模型，缺乏统计基础，结果难以直观的解释。

对于问题1，主题模型非负矩阵分解（NMF）可以解决矩阵分解的速度问题。对于问题2，这是老大难了，大部分主题模型的主题的个数选取一般都是凭经验的，较新的层次狄利克雷过程（HDP）可以自动选择主题个数。对于问题3，牛人们整出了pLSI(也叫pLSA)和隐含狄利克雷分布(LDA)这类基于概率分布的主题模型来替代基于矩阵分解的主题模型。

回到LSI本身，对于一些规模较小的问题，如果想快速粗粒度的找出一些主题分布的关系，则LSI是比较好的一个选择，其他时候，如果你需要使用主题模型，推荐使用LDA和HDP。

3.2.1、算法原理

在文本挖掘的过程中，通常使用基于单词的出现与否以及TF-IDF等进行向量空间模型的表示，而这种方式只是简单的表达了文本的向量，并未能够将语义的相似考虑进去。

我们希望找到一种模型，能够捕获到单词之间的相关性。如果两个单词之间有很强的相关性，那么当一个单词出现时，往往意味着另一个单词也应该出现(同义词)；反之，如果查询语句或者文档中的某个单词和其他单词的相关性都不大。
LSA(LSI)使用SVD来对单词-文档矩阵进行分解。SVD可以看作是从单词-文档矩阵中发现不相关的索引变量(因子)，将原来的数据映射到语义空间内。在单词-文档矩阵中不相似的两个文档，可能在语义空间内比较相似。

SVD，亦即奇异值分解，是对矩阵进行分解的一种方法，一个t*d维的矩阵(单词-文档矩阵)X，可以分解为T*S*DT，其中T为t*m维矩阵，T中的每一列称为左奇异向量(left singular bector)，S为m*m维对角矩阵，每个值称为奇异值(singular value)，D为d*m维矩阵,D中的每一列称为右奇异向量。在对单词文档矩阵X做SVD分解之后，我们只保存S中最大的K个奇异值，以及T和D中对应的K个奇异向量，K个奇异值构成新的对角矩阵S’，K个左奇异向量和右奇异向量构成新的矩阵T’和D’：$X^{’}=T^{’} \times S^{’}\times D^{’}T$形成了一个新的t*d矩阵。
这里举一个简单的LSI实例，假设我们有下面这个有11个词三个文本的词频TF对应矩阵如下：

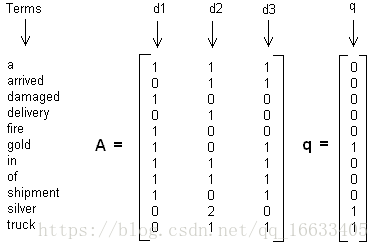
LSA01

这里我们没有使用预处理，也没有使用TF-IDF，在实际应用中最好使用预处理后的TF-IDF值矩阵作为输入。
我们假定对应的主题数为2，则通过SVD降维后得到的三矩阵为：

LSA02
从矩阵$U_k$我们可以看到词和词义之间的相关性。而从Vk可以看到3个文本和两个主题的相关性。大家可以看到里面有负数，所以这样得到的相关度比较难解释。

3.2.2、文档相似度计算

在上面我们通过LSI得到的文本主题矩阵即Vk可以用于文本相似度计算。而计算方法一般是通过余弦相似度。比如对于上面的三文档两主题的例子。我们可以计算第一个文本和第二个文本的余弦相似度如下：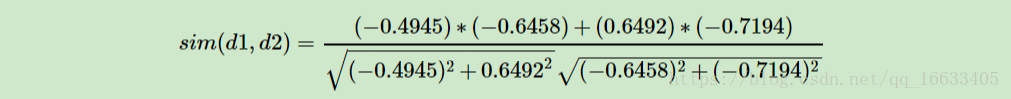
文本相似度计算(余弦)

到这里也许你对整个过程也许还有点懵逼，为什么要用SVD分解，分解后得到的矩阵是什么含义呢？别着急下面将为你解答。

潜在语义索引（Latent Semantic Indexing）与PCA不太一样，至少不是实现了SVD就可以直接用的，不过LSI也是一个严重依赖于SVD的算法，之前吴军老师在矩阵计算与文本处理中的分类问题中谈到：
“三个矩阵有非常清楚的物理含义。第一个矩阵X中的每一行表示意思相关的一类词，其中的每个非零元素表示这类词中每个词的重要性（或者说相关性），数值越大越相关。最后一个矩阵Y中的每一列表示同一主题一类文章，其中每个元素表示这类文章中每篇文章的相关性。中间的矩阵则表示类词和文章雷之间的相关性。因此，我们只要对关联矩阵A进行一次奇异值分解，w 我们就可以同时完成了近义词分类和文章的分类。（同时得到每类文章和每类词的相关性）。”

上面这段话可能不太容易理解，不过这就是LSI的精髓内容，我下面举一个例子来说明一下，下面的例子来自LSA tutorial：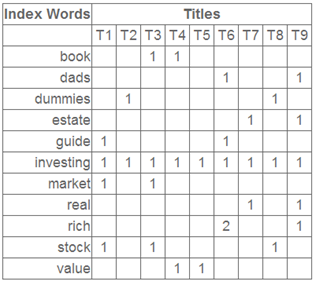

这就是一个矩阵，不过不太一样的是，这里的一行表示一个词在哪些title（文档）中出现了（一行就是之前说的一维feature），一列表示一个title中有哪些词，（这个矩阵其实是我们之前说的那种一行是一个sample的形式的一种转置，这个会使得我们的左右奇异向量的意义产生变化，但是不会影响我们计算的过程）。比如说T1这个title中就有guide、investing、market、stock四个词，各出现了一次，我们将这个矩阵进行SVD，得到下面的矩阵：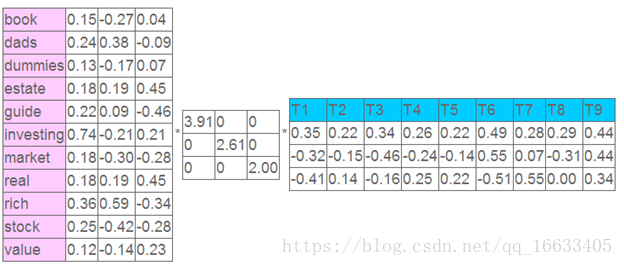
LSA tutorial01

左奇异向量表示词的一些特性，右奇异向量表示文档的一些特性，中间的奇异值矩阵表示左奇异向量的一行与右奇异向量的一列的重要程序，数字越大越重要。
继续看这个矩阵还可以发现一些有意思的东西，首先，左奇异向量的第一列表示每一个词的出现频繁程度，虽然不是线性的，但是可以认为是一个大概的描述，比如book是0.15对应文档中出现的2次，investing是0.74对应了文档中出现了9次，rich是0.36对应文档中出现了3次；
其次，右奇异向量中一的第一行表示每一篇文档中的出现词的个数的近似，比如说，T6是0.49，出现了5个词，T2是0.22，出现了2个词。
然后我们反过头来看，我们可以将左奇异向量和右奇异向量都取后2维（之前是3维的矩阵），投影到一个平面上，可以得到（如果对左奇异向量和右奇异向量单独投影的话也就代表相似的文档和相似的词）：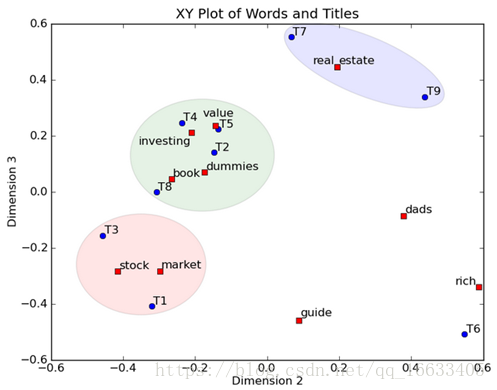
word相似性

在图上，每一个红色的点，都表示一个词，每一个蓝色的点，都表示一篇文档，这样我们可以对这些词和文档进行聚类，比如说stock 和 market可以放在一类，因为他们老是出现在一起，real和estate可以放在一类，dads，guide这种词就看起来有点孤立了，我们就不对他们进行合并了。按这样聚类出现的效果，可以提取文档集合中的近义词，这样当用户检索文档的时候，是用语义级别（近义词集合）去检索了，而不是之前的词的级别。这样一减少我们的检索、存储量，因为这样压缩的文档集合和PCA是异曲同工的，二可以提高我们的用户体验，用户输入一个词，我们可以在这个词的近义词的集合中去找，这是传统的索引无法做到的。

SVD和LSI/LSA